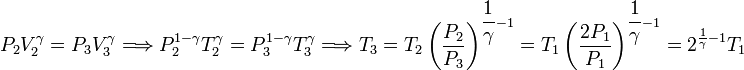Proceso isotermo y adiabático consecutivos

De Laplace

1 Enunciado

Se comprime un mol de aire en condiciones estándar mediante un proceso isotermo hasta reducir su volumen a la mitad, luego se expande adiabáticamente hasta recuperar su presión inicial. Ambos procesos son cuasiestáticos. Halle

1. La temperatura final
2. El trabajo total realizado por el gas
3. El calor total absorbido por el gas
4. La variación de energía interna

2 Solución

El gráfico representa los dos procesos a los que se somete el gas, primero una compresión isoterma y después una expansión adiabática. Analicemos cada uno de estos procesos

2.1 Compresión isoterma

Los datos que tenemos de este proceso son

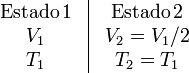
Al ser isotermo la variación de energía interna del gas es nula

El trabajo realizado es

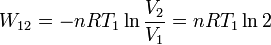
Y el calor absorbido es

2.2 Expansión adiabática

El proceso viene descrito por los parámetros

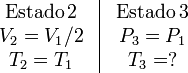
Podemos determinar P₂ usando la ley de Boyle para relacionar los estados 1 y 2

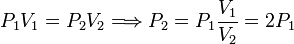
Y ahora usamos la ecuación de Poisson para relacionar los estados 2 y 3