Campo producido por una espira poligonal
De Laplace
Contenido |
1 Enunciado
Por las espira de formas irregulares de las figuras circula una corriente I. Halle el valor del campo en el punto P en cada caso.
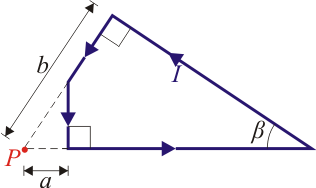
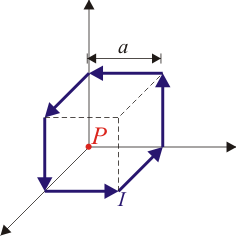
Para cada una de las espiras, hállese su momento magnético y la expresión del campo magnético y del potencial vector en puntos alejados de la espira.
2 Cuadrilátero
2.1 Campo en P
El campo es la suma de las contribuciones de cada uno de los lados del cuadrilátero. El campo de un segmento puede calcularse por integración directa, resultando la expresión
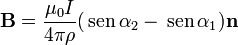
donde α1 y α2 son los ángulos con que se ven los extremos del segmento desde P, ρ es la distancia de P a la recta soporte del segmento y 
la normal al plano definido por el segmento y P, orientado según la regla de la mano derecha.
El punto P se encuentra en la intersección de la prolongación de dos de los lados. Por
