Entrar Página Discusión Historial Go to the site toolbox

Ley de Gauss para el campo magnético

De Laplace

Contenido

1 Forma diferencial

Para calcular la divergencia del campo magnético, se parte de la ley de Biot y Savart para una distribución de corriente de volumen

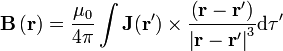
\mathbf{B}\left(\mathbf{r}\right) = \frac{\mu _0}{4\pi}\int \mathbf{J}(\mathbf{r}')\times\frac{\left(\mathbf{r} - \mathbf{r}'\right)}{\left|\mathbf{r} - \mathbf{r}'\right|^3}\mathrm{d}\tau'

y, operando se llega a que puede escribirse como

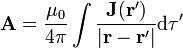
\mathbf{B}=\nabla\times\mathbf{A}        \mathbf{A}=\frac{\mu_0}{4\pi}\int\frac{\mathbf{J}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\mathrm{d}\tau'

de donde es inmediato que

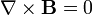
\nabla\times\mathbf{B}=0

esto es, el campo magnético es un campo solenoidal: carece de fuentes escalares. Por analogía con el caso eléctrico, denominamos a esta ecuación Ley de Gauss para el campo magnético.

Físicamente, por analogía con el campo eléctrico, podemos decir que esta ley expresa que el campo magnético carece de fuentes escalares, esto es, que no existen las cargas magnéticas (conocidas como monopolos).

Realmente, la ecuación sólo la hemos demostrado para el campo creado por corrientes estacionarias. Sin embargo, la evidencia experimental muestra que es válida siempre: para corrientes, para imanes, en situaciones estacionarias o dinámicas. Es la experiencia la que indica que no existen los monopolos.

1.1 Demostración

Para demostrar la ley de Gauss para el campo magnético partiendo de la ley de Biot y Savart, hacemos uso de la identidad

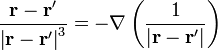
\frac{\mathbf{r} - \mathbf{r}'}{\left|\mathbf{r} - \mathbf{r}'\right|^3} = -\nabla \left(\frac{1}{\left|\mathbf{r} - \mathbf{r}' \right|} \right)

lo que nos permite escribir la ley de Biot y Savart como

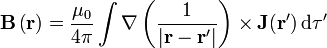
\mathbf{B}\left(\mathbf{r}\right) = \frac{\mu _0}{4\pi}\int \nabla \left(\frac{1}{\left|\mathbf{r} - \mathbf{r}' \right|} \right)\times \mathbf{J}(\mathbf{r}')\,\mathrm{d}\tau'

y aplicando la identidad vectorial

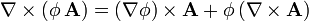
\nabla\times(\phi\,\mathbf{A})=(\nabla\phi)\times\mathbf{A}+\phi\,(\nabla\times\mathbf{A})

podemos separar el campo en dos integrales

\mathbf{B}\left(\mathbf{r}\right) = \frac{\mu _0}{4\pi}\int \nabla \times \left(\frac{\mathbf{J}(\mathbf{r}')}{\left|\mathbf{r} - \mathbf{r}' \right|} \right)\,\mathrm{d}\tau'-\frac{\mu _0}{4\pi}\int \left(\frac{\nabla\times\mathbf{J}(\mathbf{r}')}{\left|\mathbf{r} - \mathbf{r}' \right|} \right)\,\mathrm{d}\tau'

2 Forma integral

3 Condición de salto

4 ¿Son cerradas las líneas de campo magnético?

Obtenido de "http://tesla.us.es/wiki/index.php/Ley_de_Gauss_para_el_campo_magn%C3%A9tico"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace