Modelo esférico de generador
De Laplace
Contenido |
1 Enunciado
Como modelo ideal de generador suponga el siguiente sistema: una esfera de radio a de conductividad σ1 se encuentra inmersa en un medio de conductividad σ2 que se extiende hasta el infinito. En el interior de la esfera actúa una fuerza no electrostática por unidad de carga 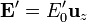 , constante y uniforme.
, constante y uniforme.
- Escriba las ecuaciones y condiciones de salto para la densidad de corriente, el campo y el potencial eléctrico en todo el espacio.
- Sabiendo que en el interior de la esfera el potencial es de la forma
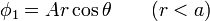
- y en el exterior de ella
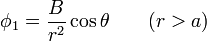
- calcule las constantes A y B.
- Halle la potencia desarrollada por el campo eléctrico en el interior y el exterior de la esfera.
- Considerando que la corriente es la que atraviesa el plano ecuatorial de la esfera (z = 0, r < a) determine la fuerza electromotriz, la resistencia interna y la externa del circuito equivalente.
- ¿A qué tienden los resultados cuando
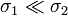 ? ¿Y cuando
? ¿Y cuando 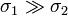 ?
?
2 Solución
2.1 Introducción
Antes de pasar a la solución matemática del problema, vamos a interpretar el sistema físicamente.
Nuestra idea es considerar el caso de un generador cuyos polos puede estar en circuito abierto o unidos por una resistencia. Un caso sencillo sería una pila de 1.5 V conectada o no a un cable.
Sabemos que en circuito abierto habrá una corriente nula y una diferencia de potencial entre bornes igual a la fuerza electromotriz. Igualmente sabemos que si se conectan los polos por un material óhmico habrá una cierta corriente fluyendo del polo positivo al negativo por el cable de conexión, y del negativo al positivo por el interior del generador.
Sin embargo, esta imagen se vuelve extremadamente complicada cuando se intentan obtener expresiones cuantitativas a partir del conocimiento del mecanismo generador y la geometría del sistema. Un modelo realista de generador implica un análisis de las fuerzas no electrostáticas implicadas, así como una complicada geometría (incluso en el caso de una simple pila de 1.5 V). Por ello, aquí consideraremos un modelo muy simplificado que mantiene los aspectos esenciales.
La forma del generador la supondremos esférica, que es la que permite mayor simplicidad en las ecuaciones. En el interior de esta esfera hay un campo efectivo que supondremos uniforme 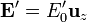 . Este campo tira de las cargas positivas y las lleva hacia la parte positiva del eje Z (“arriba”) y de las negativas hacia la parte negativa del mismo eje (“abajo”). Aparecerán entonces dos polos: el ánodo arriba y el cátodo abajo. El campo eléctrico irá de las cargas positivas a las negativas, esto es, de arriba abajo tanto dentro como fuera de la esfera.
. Este campo tira de las cargas positivas y las lleva hacia la parte positiva del eje Z (“arriba”) y de las negativas hacia la parte negativa del mismo eje (“abajo”). Aparecerán entonces dos polos: el ánodo arriba y el cátodo abajo. El campo eléctrico irá de las cargas positivas a las negativas, esto es, de arriba abajo tanto dentro como fuera de la esfera.
Para modelar las resistencias del circuito consideraremos que tanto el interior como el exterior pueden caracterizarse por sendas conductividades. La de dentro da la proporcionalidad entre la corriente interior y el campo total (eléctrico más efectivo) mientras que la de fuera relaciona la corriente exterior con el campo eléctrico exterior. Así, en lugar de considerar que los polos están conectados por un cable, nos imaginamos que el generador está sumergido en un líquido óhmico, de forma que todo el exterior funciona como el cable de conexión.
la corriente eléctrica, entonces, irá de abajo arriba por el interior (ya que el campo efectivo es mayor que el eléctrico) y de arriba abajo por el exterior.
Una vez que hagamos los cálculos, podremos sustituir el sistema por un circuito equivalente, consistente en una fuente ideal, una resistencia interna y una externa.
2.2 Ecuaciones y condiciones de salto
2.2.1 Ecuaciones
El sistema está formado por dos regiones: la interior (“1”) en r < a, y la exterior (“2”) en r > a. En cada una de ellas tendremos un cierto campo eléctrico 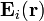 , que debemos determinar.
, que debemos determinar.
Por tratarse de una situación estacionaria, el campo eléctrico en cada región es irrotacional
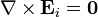

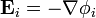
Igualmente, por ser la corrientes estacionarias, las densidades de corriente cumplen
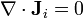
Para completar estas relaciones, precisamos de las relaciones constitutivas, que indicamos después.
2.2.2 Condiciones de salto
En la frontera entre las dos regiones debe cumplirse la continuidad de la componente tangencial del campo eléctrico, que implica la continuidad del potencial eléctrico
![\mathbf{n}\times[\mathbf{E}]=\mathbf{0}\qquad(r=a)](/wiki/images/math/9/3/9/939ccb995a414c4d3e44a88b806d22b7.png)

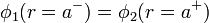
Por ser una situación estacionaria, no hay variación en la carga superficial y, por tratarse de materiales óhmicos, tampoco hay corrientes superficiales, con lo que la condición de salto para la densidad de corriente se reduce a
![\mathbf{n}\cdot[\mathbf{J}]=0\qquad(r=a)](/wiki/images/math/8/e/f/8ef518b382e26b50f35532d55f94a2c6.png)
En esta condición de salto y en la anterior, el vector  es el normal a la superficie esférica, esto es
es el normal a la superficie esférica, esto es
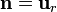
Además de estas condiciones de salto hay que imponer que el potencial eléctrico tiende a 0 en el infinito y que no es singular en el centro de la esfera (en el que no hay carga puntual alguna)


2.2.3 Relaciones constitutivas
Para completar las ecuaciones y condiciones anteriores, necesitamos ecuaciones que liguen la densidad de corriente con el campo eléctrico.
En el exterior del generador esférico, la relación es simplemente la ley de Ohm


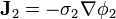
En el interior del generador no se cumple estrictamente la ley de Ohm, ya que las cargas no son movidas solamente por el campo electrostático, sino que también actúa sobre ellas el campo efectivo 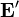 que es el que consigue vencer al campo eléctrico y separar las cargas. La densidad de corriente estará asociada a la superposición de estos efectos a través de una generalización de la ley
que es el que consigue vencer al campo eléctrico y separar las cargas. La densidad de corriente estará asociada a la superposición de estos efectos a través de una generalización de la ley
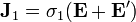
2.2.4 Ecuaciones para el potencial
Combinando todo lo anterior podemos expresar el problema como uno para el potencial eléctrico. Tenemos que en el exterior del generador el potencial cumple la ecuación de Laplace


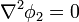
En coordenadas esféricas queda
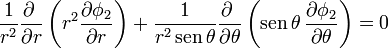
No se han incluido el término con derivadas en  porque, dada la simetría del sistema (de revolución en torno al eje Z), el potencial no va a depender de esta coordenada. Sí va a depender de θ ya que no es lo mismo estar por el lado del ánodo que por el del cátodo.
porque, dada la simetría del sistema (de revolución en torno al eje Z), el potencial no va a depender de esta coordenada. Sí va a depender de θ ya que no es lo mismo estar por el lado del ánodo que por el del cátodo.
En el interior también se cumple la ecuación de Laplace, por ser 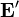 un campo uniforme
un campo uniforme
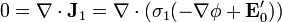

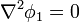
y la expresión en coordenadas esféricas es idéntica a la que escribimos antes.
Si en las ecuaciones diferenciales para el potencial no aparece el campo efectivo, cabe preguntarse dónde lo hace. Es en las condiciones de salto donde es necesario incluirlo. En términos físicos, la consecuencia de que haya un 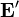 es la aparición de una densidad de carga que en este simple modelo estará en la superficie de la esfera.
es la aparición de una densidad de carga que en este simple modelo estará en la superficie de la esfera.
En esta superficie (r = a) se cumple la continuidad del potencial
![[\phi]=0\,](/wiki/images/math/8/a/f/8af700183719a53d501011821f5f54cf.png)

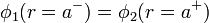
y de la componente normal de la corriente eléctrica
![\mathbf{n}\cdot[\mathbf{J}]=0\,](/wiki/images/math/a/6/f/a6f53d3c4857da79d4ee93323277a0f2.png)

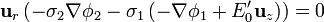


Además tenemos las dos condiciones de contorno


2.3 Potencial eléctrico
2.3.1 Expresión general del potencial
Aunque el propio enunciado da la expresión de las soluciones para el potencial, podemos inducir éstas directamente a partir de la ecuación de Laplace y del conocimiento de diferentes sistemas electrostáticos.
Comenzamos separando la dependencia radial de la angular. Si examinamos las ecuaciones y condiciones de salto anteriores, vemos que la única dependencia angular aparece como un cosθ en una condición de salto. Por ello, y protegidos en la retaguardia por el teorema de unicidad, proponemos la solución

donde, tras sustituir en la ecuación de Laplace, la función f(r) verifica la ecuación diferencial

La solución de esta ecuación será una función, dependiente solo de r y de dos constantes de integración. Podemos hallar esta función resolviendo la ecuación diferencial (que es una de las llamadas equidimensionales o de Euler). No obstante, es más intructivo aprovechar las soluciones que ya conocemos.
Existen dos potenciales proporcionales a cosθ:
- El potencial de un campo uniforme en la dirección del eje Z
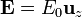


- El potencial de un dipolo que apunta según el mismo eje

Estos dos potenciales cumplen la ecuación de Laplace y son iguales a una función de r multiplicada por el coseno del ángulo polar. Por ello, la solución general para esta dependencia angular la podemos escribir como
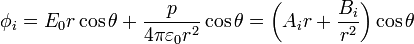
donde Ai y Bi son las constantes de integración, a determinar a partir de las condiciones de salto y de contorno. Una vez halladas, puede interpretarse el resultado en términos de campos uniformes y momentos dipolares.
2.3.2 Cálculo de las constantes
El potencial en el interior y el exterior del generador tiene en principio la misma forma
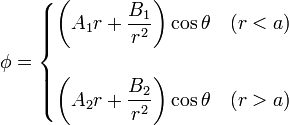
Debemos hallar cuatro constantes, para lo cual disponemos de dos condiciones de salto y dos de contorno.
2.3.2.1 Anulación en el infinito
Puesto que el potencial se anula lejos del generador, debe ser


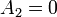
ya que el término A2rcosθ diverge lejos de la esfera generadora.
2.3.2.2 No divergencia en el centro
En el centro de la esfera el potencial no es singular
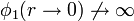

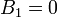
ya que un término en 1 / r2 es divergente en 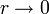 .
.
2.3.2.3 Continuidad del potencial
Hemos demostrado ya que el potencial se reduce a la expresión dada en el enunciado
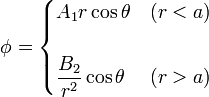
lo cual nos dice que el campo eléctrico en el interior del generador es uniforme, mientras que en el exterior se trata de un campo dipolar.
Imponiendo ahora la continuidad del potencial en la superficie del generador
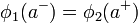

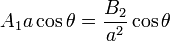

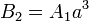
2.3.2.4 Continuidad de la corriente
Imponiendo por último la continuidad de la componente normal de la densidad de corriente


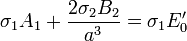
2.3.3 Solución para el potencial
Las dos condiciones de salto nos dan finalmente
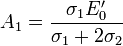
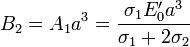
y la expresión para el potencial en todo el espacio es
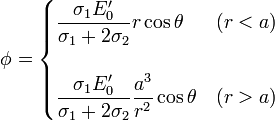
2.3.4 Campo eléctrico
Una vez que tenemos el potencial podemos hallar el campo, que, como sabemos, será uniforme en el interior de la esfera y dipolar en el exterior.
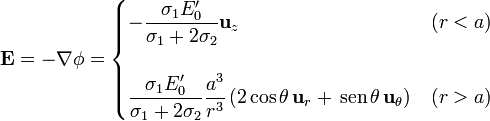
Vemos que, como corresponde a un generador, el campo en el interior de éste va en sentido opuesto al campo efectivo.
2.3.5 Densidad de corriente
Para hallar la densidad de corriente, debemos distinguir el interior y el exterior del generador. En el interior

y en el exterior
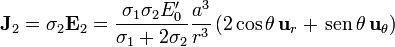
A diferencia del campo eléctrico, la densidad de corriente en el interior del generador sí va en el sentido del campo efectivo (y opuesta, por tanto, al campo eléctrico).
2.4 Potencia eléctrica
La potencia desarrollada por el campo eléctrico es igual a
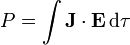
En esta expresión el campo efectivo aparece en la densidad de corriente, ya que podemos d
2.5 Circuito equivalente
2.6 Valores límite
Podemos interpretar los resultados anteriores con





