Segunda Convocatoria Ordinaria 2016/17 (MR G.I.C.)

De Laplace

Disco sobre barra en forma de L

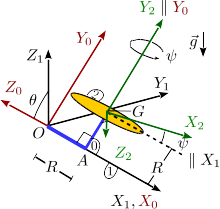
El disco homogéneo de la figura (sólido "2") tiene masa m y radio R. Está conectado por su centro G con una estructura (sólido "0") formada por dos barras perpendiculares de masas despreciables y longitud R cada una. El disco puede rotar alrededor del eje AG, mientras que el sólido "0" puede rotar respecto a la línea OA. Se escoge unos ejes intermedios OX₀Y₀Z₀ de modo que el plano OX₀Y₀ contiene siempre al sólido "0" y al centro del disco G. Los ejes GX₂Y₂Z₂ son solidarios con el disco. El eje GY₂ es paralelo al eje OY₀, por lo que el plano GX₂Z₂ es siempre paralelo al plano OX₀Z₀ y el eje GX₂ forma un ángulo ψ con la dirección del eje X₁. El sistema está sometido a la acción de la gravedad con la dirección y sentido indicada en la figura.

1. Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21} en el centro de masas del disco, así como la derivada temporal del {21}. Determina el eje instantáneo de rotación del movimiento {21}.
2. Calcula el momento cinético del disco respecto a G, su energía cinética y su energía potencial.
3. Encuentra las integrales primeras del movimiento que puedas, justificando porqué lo son.
4. Supongamos a partir de ahora que θ = π / 2 en todo instante.¿Como es la reducción cinemática {21} en G y su derivada temporal?
5. En este último caso, calcula la desvinculación global {21} en G. Aplicando los teoremas fundamentales, encuentra la ecuación de movimiento para el grado de libertad restante.