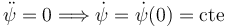De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

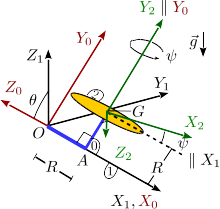
El disco homogéneo de la figura (sólido "2") tiene masa $m$ y radio $R$ . Está conectado por su centro $G$ con una estructura (sólido "0") formada por dos barras perpendiculares de masas despreciables y longitud $R$ cada una. El disco puede rotar alrededor del eje $A G$ , mientras que el sólido "0" puede rotar respecto a la línea $O A$ . Se escoge unos ejes intermedios $O X 0 Y 0 Z 0$ de modo que el plano $O X 0 Y 0$ contiene siempre al sólido "0" y al centro del disco $G$ . Los ejes $G X 2 Y 2 Z 2$ son solidarios con el disco. El eje $G Y 2$ es paralelo al eje $O Y 0$ , por lo que el plano $G X 2 Z 2$ es siempre paralelo al plano $O X 0 Z 0$ y el eje $G X 2$ forma un ángulo $ψ$ con la dirección del eje $X 1$ . El sistema está sometido a la acción de la gravedad con la dirección y sentido indicada en la figura.

Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21} en el centro de masas del disco, así como la derivada temporal del {21}. Determina el eje instantáneo de rotación del movimiento {21}.
Calcula el momento cinético del disco respecto a $G$ , su energía cinética y su energía potencial.
Encuentra las integrales primeras del movimiento que puedas, justificando porqué lo son.
Supongamos a partir de ahora que $θ = π / 2$ en todo instante.¿Como es la reducción cinemática {21} en $G$ y su derivada temporal?
En este último caso, calcula la desvinculación global {21} en G. Aplicando los teoremas fundamentales, encuentra la ecuación de movimiento para el grado de libertad restante.

2 Solución

2.1 Reducciones cinemáticas

2.1.1 Movimiento {01}

La línea $O A$ es fija. Tenemos

$\vec{v}^{\,O}_{01} = \vec{0}, \qquad \vec{\omega}_{01} = \dot{\theta}\,\vec{\imath}_0$

La derivada temporal es

$\vec{a}^{\,O}_{01} = \vec{0},\qquad \vec{\alpha}_{01} = \ddot{\theta}\,\vec{\imath}_0$

2.1.2 Movimiento {20}

Esto es una rotación de eje permanente $G Y 0$

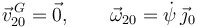
$\vec{v}^{\,G}_{20} = \vec{0}, \qquad \vec{\omega}_{20} = \dot{\psi}\,\vec{\jmath}_0$

La derivada temporal es

$\vec{a}^{\,G}_{20} = \vec{0},\qquad \vec{\alpha}_{20} = \ddot{\psi}\,\vec{\jmath}_0$

2.1.3 Movimiento {21}

Usamos las leyes de composición

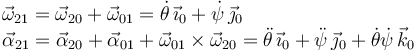
$\begin{array}{l} \vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} = \dot{\theta}\,\vec{\imath}_0 + \dot{\psi}\,\vec{\jmath}_0 \\ \vec{\alpha}_{21} = \vec{\alpha}_{20} + \vec{\alpha}_{01} + \vec{\omega}_{01}\times\vec{\omega}_{20} = \ddot{\theta}\,\vec{\imath}_0 + \ddot{\psi}\,\vec{\jmath}_0 + \dot{\theta}\dot{\psi}\,\vec{k}_0 \end{array}$

Para las velocidades y aceleraciones absolutas de $G$ tenemos

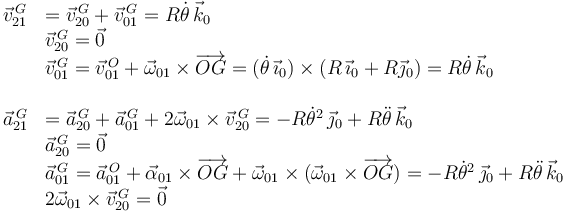
$\begin{array}{ll} \vec{v}^{\,G}_{21} & = \vec{v}^{\,G}_{20} + \vec{v}^{\,G}_{01} = R\dot\theta\,\vec{k}_0\\ & \vec{v}^{\,G}_{20} = \vec{0}\\ & \vec{v}^{\,G}_{01} = \vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OG}= (\dot{\theta}\,\vec{\imath}_0)\times(R\,\vec{\imath}_0 + R\vec{\jmath}_0) = R\dot\theta\,\vec{k}_0\\ &\\ \vec{a}^{\,G}_{21} & = \vec{a}^{\,G}_{20} + \vec{a}^{\,G}_{01} + 2\vec{\omega}_{01}\times\vec{v}^{\,G}_{20} = -R\dot{\theta}^2\,\vec{\jmath}_0 + R\ddot\theta\,\vec{k}_0\\ & \vec{a}^{\,G}_{20} = \vec{0}\\ & \vec{a}^{\,G}_{01} = \vec{a}^{\,O}_{01} + \vec{\alpha}_{01}\times\overrightarrow{OG} + \vec{\omega}_{01}\times(\vec{\omega}_{01}\times\overrightarrow{OG})= -R\dot{\theta}^2\,\vec{\jmath}_0 + R\ddot\theta\,\vec{k}_0\\ & 2\vec{\omega}_{01}\times\vec{v}^{\,G}_{20} = \vec{0} \end{array}$

Para localizar un punto del eje $Δ 21$ hacemos

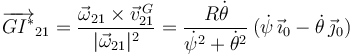
$\overrightarrow{GI^*}_{21} = \dfrac{\vec{\omega}_{21}\times\vec{v}^{\,G}_{21}}{|\vec{\omega}_{21}|^2} = \dfrac{R\dot{\theta}}{\dot{\psi}^2+\dot{\theta}^2}\,(\dot{\psi}\,\vec{\imath}_0 -\dot{\theta}\,\vec{\jmath}_0)$

El movimiento {21} es una rotación pura pues

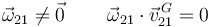
$\vec{\omega}_{21}\neq \vec{0}\,\qquad \vec{\omega}_{21}\cdot\vec{v}^{\,G}_{21}=0$

2.2 Cinética

El tensor de inercia en $G$ es

$\overset\leftrightarrow{I}_G = I \left[ \begin{array}{ccc} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 1 \end{array} \right]_0 \qquad\qquad I = mR^2/4$

En principio el tensor de inercia debe expresarse en el sistema "2", solidario con el disco. Pero los ejes $G Y 0$ y $G Y 2$ coinciden, y el disco tiene simetría de revolución alrededor de ellos. Por tanto, cualquier par de ejes perpendiculares a $G Y 0$ es un par de ejes principales. Por tanto, podemos usar el sistema "0" para calcular el momento cinético. Tenemos entonces

$\vec{L}_{G} = \overset\leftrightarrow{I}_G\cdot\vec{\omega}_{21} = \overset\leftrightarrow{I}_G = I \left[ \begin{array}{ccc} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 1 \end{array} \right]_0 \left[ \begin{array}{c} \dot{\theta} \\ \dot{\psi} \\ 0 \end{array} \right]_0 = \left[ \begin{array}{c} I\dot{\theta} \\ 2I\dot{\psi} \\ 0 \end{array} \right]_0$

La energía cinética consta de la parte de traslación del centro de masas y de rotación

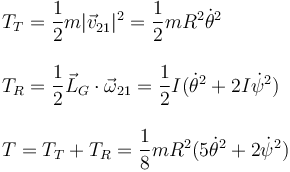
$\begin{array}{l} T_{T} = \dfrac{1}{2}m|\vec{v}^{\,}_{21}|^2 = \dfrac{1}{2}mR^2\dot{\theta}^2\\ \\ T_{R} = \dfrac{1}{2}\vec{L}_G\cdot\vec{\omega}_{21} = \dfrac{1}{2}I(\dot{\theta}^2+2I\dot{\psi}^2) \\ \\ T = T_{T} + T_R = \dfrac{1}{8}mR^2(5\dot{\theta}^2+2\dot{\psi}^2) \end{array}$

Para la energía potencial gravitatoria tomamos como origen el plano $O X 1 Y 1$ . Tenemos

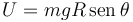
$U = mgR\,\mathrm{sen}\,\theta$

2.3 Integrales primeras del movimiento

Las fuerzas y pares vinculares no hacen trabajo. Sólo el peso hace trabajo. Entonces se conserva la energía mecánica.

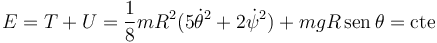
$E = T + U = \dfrac{1}{8}mR^2(5\dot{\theta}^2+2\dot{\psi}^2) + mgR\,\mathrm{sen}\,\theta = \mathrm{cte}$

Las fuerzas que actúan sobre el disco son el peso y la fuerza vincular de la barra, ambas aplicadas en $G$ . Hay un par de fuerzas vincular ejercido por la barra

$\vec{\Gamma}_{20} = [\Gamma_x, 0, \Gamma_z]_0$

Así pues, las fuerzas sobre el disco cortan al eje $G Y 0$ y el par vincular no tiene componente sobre este eje. Entonces, la proyección del momento angular sobre ese eje se conserva

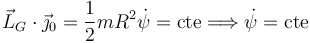
$\vec{L}_G\cdot\vec{\jmath}_0 = \dfrac{1}{2}mR^2\dot{\psi}=\mathrm{cte} \Longrightarrow \dot{\psi}=\mathrm{cte}$

2.4 Caso $θ = π / 2$

En esta situación los ejes del sistema "0" coinciden con los del "1". Tenemos

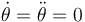
$\dot{\theta} = \ddot{\theta}=0$

La reducción cinemática pedida es

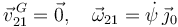
$\vec{v}^{\,G}_{21} = \vec{0}, \quad \vec{\omega}_{21} = \dot{\psi}\,\vec{\jmath}_0$

Su derivada es

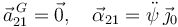
$\vec{a}^{\,G}_{21} = \vec{0}, \quad \vec{\alpha}_{21} = \ddot{\psi}\,\vec{\jmath}_0$

El movimiento es simplemente una rotación alrededor de su eje de simetría fijo.

2.4.1 Desvinculación global y ecuación de movimiento

De la reducción cinemática obtenemos que la reducción vincular en este caso simplificado es

$\vec{\Phi}^{\,G}_{21} = [ G_x, G_y, G_z]_0, \qquad \vec{\Gamma}_{21} = [\Gamma_x, 0, \Gamma_z]_0$

Podemos obtener una ecuación para el grado de libertad de movimiento aplicando el Teorema del Momento Cinético en el centro de masas del disco

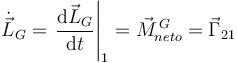
$\dot{\vec{L}}_G = \left.\dfrac{\mathrm{d}\vec{L}_G}{\mathrm{d}t}\right|_1 = \vec{M}^{\,G}_{neto} = \vec{\Gamma}_{21}$

En este caso los sistemas "0" y "1" coinciden en todo instante de tiempo. Por tanto

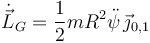
$\dot{\vec{L}}_G = \dfrac{1}{2}mR^2\ddot{\psi}\,\vec{\jmath}_{0,1}$

Como la componente en 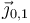$\vec{\jmath}_{0,1}$ del par neto es nula, tenemos

$\ddot{\psi}=0 \Longrightarrow \dot{\psi}= \dot{\psi}(0) = \mathrm{cte}$

Disco sobre barra en forma de L (MR G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Reducciones cinemáticas

2.1.1 Movimiento {01}

2.1.2 Movimiento {20}

2.1.3 Movimiento {21}

2.2 Cinética

2.3 Integrales primeras del movimiento

2.4 Caso $θ = π / 2$

2.4.1 Desvinculación global y ecuación de movimiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Disco sobre barra en forma de L (MR G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Reducciones cinemáticas

2.1.1 Movimiento {01}

2.1.2 Movimiento {20}

2.1.3 Movimiento {21}

2.2 Cinética

2.3 Integrales primeras del movimiento

2.4 Caso θ = π / 2

2.4.1 Desvinculación global y ecuación de movimiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.4 Caso $θ = π / 2$