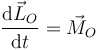Magnitudes en una máquina de Atwood

De Laplace

Revisión a fecha de 12:07 13 ago 2015; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Propiedades del sistema
3 Leyes de evolución

1 Enunciado

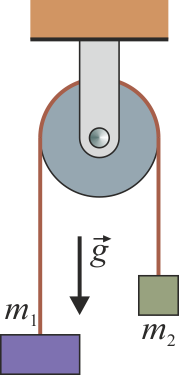
Considere una máquina de Atwood ideal formada por dos masas $m 1$ y $m 2$ que cuelgan de una polea (ideal, sin rozamiento ni masa) de radio $b$ a través de un hilo también ideal (inextensible y sin masa) de longitud $l$ ). Inicialmente las dos masas están en reposo a la misma altura.

Determine la masa total, la posición, velocidad y aceleración del centro de masas, la cantidad de movimiento, el momento cinético respecto al centro de la polea y la energía cinética del sistema, todo ello como función del tiempo.
Para la cantidad de movimiento, el momento cinético respecto al centro de la polea y la energía cinética determine sus derivadas respecto al tiempo y compruebe que se satisfacen las leyes para su evolución.

2 Propiedades del sistema

2.1 Masa

La masa del sistema es simplemente la suma de las masas de las dos pesas, al ser ideal el resto del sistema.

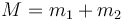
$M = m_1+m_2\,$

2.2 Propiedades del CM

2.2.1 Posición

Tomando como eje Z el vertical y hacia arriba, pero con $z = 0$ a la altura de la polea (es decir, que las coordenadas de ambas posiciones tendrán valores de z negativos), las posiciones de las dos masas son

$\vec{r}_1 = -b\vec{\imath}+z_1\vec{k}\qquad\qquad \vec{r}_2 = +b\vec{\imath}+z_2\vec{k}$

A partir de aquí, la posición del centro de masas queda

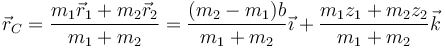
$\vec{r}_C = \frac{m_1\vec{r}_1+m_2\vec{r}_2}{m_1+m_2}=\frac{(m_2-m_1)b}{m_1+m_2}\vec{\imath}+\frac{m_1z_1+m_2z_2}{m_1+m_2}\vec{k}$

Si suponemos que inicialmente las dos masas están en reposo a la misma altura y que son aceleradas por la diferencia de pesos, con aceleración

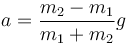
$a = \frac{m_2-m_1}{m_1+m_2}g$

tal como se ve en al estudiar la máquina de Atwood, podemos escribir la posición vertical de cada una como

$z_1= z_0+\frac{1}{2}at^2\qquad\qquad z_2 = z_0-\frac{1}{2}at^2$

lo que da la posición del CM

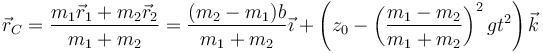
$\vec{r}_C = \frac{m_1\vec{r}_1+m_2\vec{r}_2}{m_1+m_2}=\frac{(m_2-m_1)b}{m_1+m_2}\vec{\imath}+\left(z_0-\left(\frac{m_1-m_2}{m_1+m_2}\right)^2gt^2\right)\vec{k}$

Vemos que el CM desciende aceleradamente, independientemente de cuál sea la masa más pesada.

2.2.2 Velocidad

Derivando en la posición anterior, resulta la velocidad del CM,

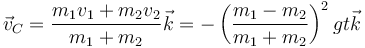
$\vec{v}_C = \frac{m_1v_1+m_2v_2}{m_1+m_2}\vec{k}=-\left(\frac{m_1-m_2}{m_1+m_2}\right)^2gt\vec{k}$

2.2.3 Aceleración

Derivando de nuevo queda

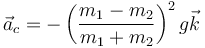
$\vec{a}_c = -\left(\frac{m_1-m_2}{m_1+m_2}\right)^2g\vec{k}$

2.3 Cantidad de movimiento

La cantidad de movimiento del sistema es proporcional a la velocidad del CM

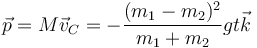
$\vec{p}=M\vec{v}_C = -\frac{(m_1-m_2)^2}{m_1+m_2}gt\vec{k}$

2.4 Momento cinético

El momento cinético es la suma de los momentos cinétiocos individuales

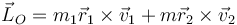
$\vec{L}_O = m_1\vec{r}_1\times \vec{v}_1 +m\vec{r}_2\times\vec{v}_2$

y resulta

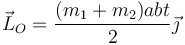
$\vec{L}_O = \frac{(m_1+m_2)ab t}{2}\vec{\jmath}$

Sustituyendo aquí el valor de la aceleración

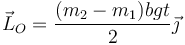
$\vec{L}_O = \frac{(m_2-m_1)bgt}{2}\vec{\jmath}$

2.5 Energía cinética

A partir de las velocidades individuales hallamos la energía cinética total

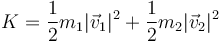
$K = \frac{1}{2}m_1|\vec{v}_1|^2+\frac{1}{2}m_2|\vec{v}_2|^2$

que da

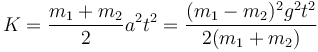
$K = \frac{m_1+m_2}{2}a^2t^2 = \frac{(m_1-m_2)^2 g^2 t^2}{2(m_1+m_2)}$

2.6 Energía potencial gravitatoria

También puede hallarse la energía potencial debida al peso del sistema

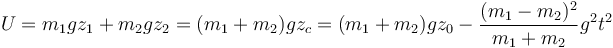
$U = m_1gz_1+m_2gz_2 = (m_1+m_2)gz_c = (m_1+m_2)gz_0-\frac{(m_1-m_2)^2}{m_1+m_2}g^2t^2$

3 Leyes de evolución

3.1 Cantidad de movimiento

Para la cantidad de movimiento del sistema se cumple

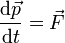
$\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=\vec{F}$

siendo $\vec{F}$ la resultante de las fuerzas externas que actúan en el sistema. En este caso, las fuerzas externas son el peso de cada masa, pero también la reacción que ejerce el soporte que sostiene la polea.

Derivando la cantidad de movimiento del sistema

$\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}= -\frac{(m_1-m_2)^2}{m_1+m_2}g\vec{k}$

Las fuerzas externas suman

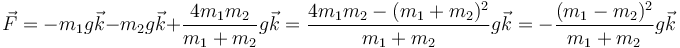
$\vec{F}=-m_1g\vec{k}-m_2g\vec{k}+\frac{4m_1m_2}{m_1+m_2}g\vec{k} =\frac{4m_1m_2-(m_1+m_2)^2}{m_1+m_2}g\vec{k}=-\frac{(m_1-m_2)^2}{m_1+m_2}g\vec{k}$

cumpliéndose la igualdad buscada.

3.2 Momento cinético

Para el momento cinético del sistema respecto al punto de anclaje, la ley es

$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\vec{M}_O$

3.3 Energía cinética

Magnitudes en una máquina de Atwood

De Laplace

Contenido

1 Enunciado

2 Propiedades del sistema

2.1 Masa

2.2 Propiedades del CM

2.2.1 Posición

2.2.2 Velocidad

2.2.3 Aceleración

2.3 Cantidad de movimiento

2.4 Momento cinético

2.5 Energía cinética

2.6 Energía potencial gravitatoria

3 Leyes de evolución

3.1 Cantidad de movimiento

3.2 Momento cinético

3.3 Energía cinética

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES