Primera convocatoria 2014/15 (F2GIA)

De Laplace

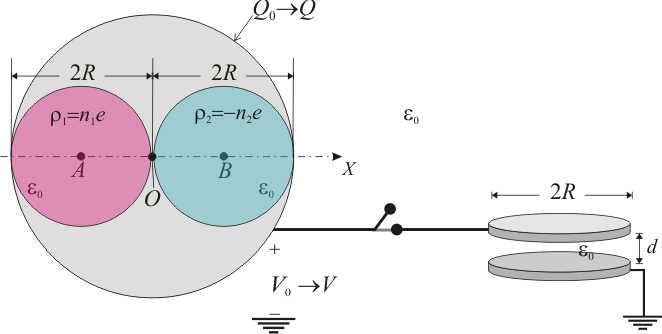
Esfera con huecos cargados y condensador

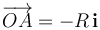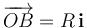Una esfera conductora de radio 2R y centro O tiene practicados en su interior dos huecos esféricos tangentes pero no conectados, ambos de radio R, de centros A y B, de manera que , y . Inicialmente, los huecos están vacíos y la esfera descargada.

Se procede a introducir en los huecos sendos gases ionizados, con iones de distinto signo y en concentraciones n₁ y n₂ lo suficientemente bajas como para poder considerar que las correspondientes cargas eléctricas se distribuyen uniformemente en cada uno de los volúmenes; así en el hueco de centro A hay una densidad volumétrica de carga constante 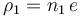, y en la de centro B, es .

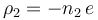Obtenga las expresiones de las magnitudes que se indican a continuación, en función de los parámetros descritos, una vez que el sistema recupera el equilibrio electrostático

a) Carga eléctrica libre, Q₀, en la superficie exterior de la esfera conductora, y densidad superficial que describe su distribución.

b) Campo eléctrico dentro de cada uno de los huecos con gas ionizado.

c) Valor V₀ del potencial electrostático a que se encuentra la esfera conductora. Diferencia de potencial entre los centros A y B de los huecos.

A continuación, la esfera se conecta mediante un cable conductor muy largo a un disco conductor de radio R, que se encuentra separado una distancia d de otro disco idéntico conectado a tierra, formando ambos un condensador plano paralelo. El espacio entre los discos está relleno de aire.

En este nuevo sistema...

d) ¿Qué relación deben verificar R y d para que la carga Q₀ de la superficie conductora se reparta a partes iguales entre ésta y el disco del condensador al cuál está conectada?

e) Determine la expresión del potencial electrostático V en la esfera conductora y el disco, en función de los parámetros R y d.

f) Considérese el caso 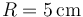y 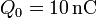. Determine el valor mínimo posible para la distancia d de separación entre discos.

Datos: carga elemental: 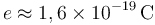;     campo de ruptura dieléctrica del aire, 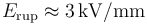.