Divergencia de un campo vectorial

De Laplace

1 Introducción

2 Definición

Se define la divergencia de un campo vectorial en un punto como el límite

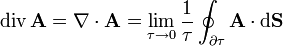
donde el límite se toma sobre volúmenes τ cada vez más pequeños que tienden al punto

3 Fuentes escalares de un campo vectorial

4 Campo solenoidal

5 Expresión de la divergencia

6 Ejemplos

7 Teorema de Gauss