Base vectorial girada
De Laplace
Revisión a fecha de 09:51 2 oct 2014; Antonio (Discusión | contribuciones)
Enunciado
Considere la terna de vectores
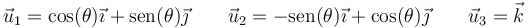
- Pruebe que constituyen una base ortonormal dextrógira. ¿Cómo están situados estos vectores?
- Halle la transformación inversa, es decir, exprese
como combinación de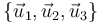 
.
- Para el caso particular en que tg(θ) = 3 / 4, particularice las ecuaciones de transformación y exprese el vector
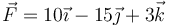en la nueva base.
