Fuerza sobre una partícula semiesférica

De Laplace

1 Enunciado

Se trata de hallar el campo eléctrico necesario para elevar en el aire una partícula metálica que reposa sobre un plano a tierra. La partícula conductora la podemos modelar como un hemisferio de radio a. Existe un campo eléctrico impuesto que, en puntos alejados de la semiesfera, es uniforme y perpendicular al plano conductor, .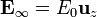

El potencial en todos los puntos por encima del plano y la partícula es de la forma

        

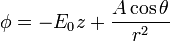
siendo r la distancia al centro de la semiesfera.

1. Determine el valor de A que hace que se satisfagan todas las ecuaciones y condiciones de contorno.
2. Halle la densidad de carga en la superficie de la semiesfera.
3. Calcule la presión electrostática en la superficie de la partícula. A partir de esta presión, halle la fuerza eléctrica sobre la partícula, empleando la relación .
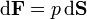4. Si la partícula es de aluminio y su radio vale 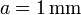, ¿qué campo es preciso para levantar esta partícula?

2 Solución