Tiro parabólico en pendiente

De Laplace

1 Enunciado

Un mortero lanza un proyectil esférico de acero de 5 cm de radio desde un punto sobre el suelo horizontal al pie de una pendiente cuya superficie forma un ángulo 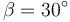con la horizontal. El mortero dispara el proyectil con una velocidad de 21 m/s. Desprecie el rozamiento con el aire y el posible efecto de rotación de la esfera.

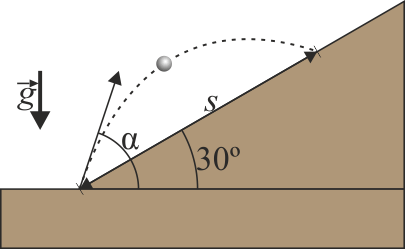
1. Si el proyectil es lanzado con un ángulo α con la horizontal, ¿a qué distancia s del mortero, medida sobre la pendiente, impacta con el suelo?
2. Halle el valor de α que hace máxima esta distancia.
3. Suponga que el proyectil se lanza con un ángulo de π/3 con la horizontal. Para este caso, halle:
   1. La rapidez que tiene en el momento del impacto.
   2. La aceleración tangencial y normal (escalares) en el momento de impacto.
   3. La variación en la energía cinética y en la potencial respecto al instante inicial.

Datos: Aceleración de la gravedad 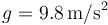. Densidad de masa del acero: .

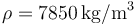2 Alcance general

En el movimiento del proyectil, se cumplen las ecuaciones horarias

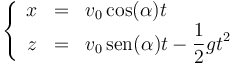
Por otro lado, en el momento de impacto, el proyectil se encuentra sobre la pendiente, por lo que

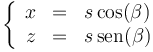
Para hallar el punto de impacto, primero despejamos el tiempo de impacto

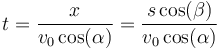
y a continuación sustituimos en la coordenada vertical

3 Alcance máximo

4 Caso particular

4.1 Rapidez de impacto

4.2 Componentes intrínsecas de la aceleración

4.3 Variación de la energía