Tiro parabólico en pendiente
De Laplace
Contenido |
1 Enunciado
Un mortero lanza un proyectil esférico de acero de 5 cm de radio desde un punto sobre el suelo horizontal al pie de una pendiente cuya superficie forma un ángulo 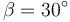 con la horizontal. El mortero dispara el proyectil con una velocidad de 21 m/s. Desprecie el rozamiento con el aire y el posible efecto de rotación de la esfera.
con la horizontal. El mortero dispara el proyectil con una velocidad de 21 m/s. Desprecie el rozamiento con el aire y el posible efecto de rotación de la esfera.
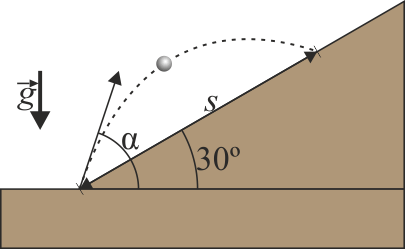
- Si el proyectil es lanzado con un ángulo α con la horizontal, ¿a qué distancia s del mortero, medida sobre la pendiente, impacta con el suelo?
- Halle el valor de α que hace máxima esta distancia.
- Suponga que el proyectil se lanza con un ángulo de π/3 con la horizontal. Para este caso, halle:
- La rapidez que tiene en el momento del impacto.
- La aceleración tangencial y normal (escalares) en el momento de impacto.
- La variación en la energía cinética y en la potencial respecto al instante inicial.
Datos: Aceleración de la gravedad 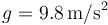 .
.
2 Alcance general
En el movimiento del proyectil, se cumplen las ecuaciones horarias
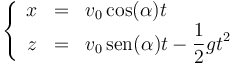
Por otro lado, en el momento de impacto, el proyectil se encuentra sobre la pendiente, por lo que
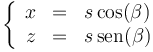
Para hallar el punto de impacto, debemos resolver este sistema de dos ecuaciones con dos incógnitas (t y s), lo cual se puede hacer de diversas formas. Una vez que hayamos calculado el alcance, buscaremos su valor máximo con respecto al ángulo de lanzamiento.
Primero despejamos el tiempo de impacto
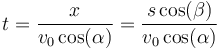
y a continuación sustituimos en la coordenada vertical

Dividiendo por s en cada miembro obtenemos una ecuación de primer grado

Despejamos de aquí el alcance

Esta expresión se puede simplificar con ayuda de las relaciones trigonométricas y escribirse como
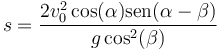
A modo de comprobación, vemos que para un plano horizontal se obtiene el resultado conocido

3 Alcance máximo
Podemos hallar el alcance máximo sin necesidad de derivar e igualar a cero con ayuda de la relación trigonométrica
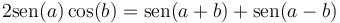
que en este caso da

En esta expresión la única dependencia en α está en el numerador. Por tanto, el máximo valor del alcance lo obtenemos cuando ese seno es igual a la unidad
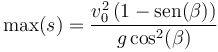
que se da para

Podemos simplificar el máximo alcance haciendo uso de otra relación trigonométrica
y queda

Comprobamos los casos límite conocidos
- Para el plano horizontal β = 0 y resulta el ángulo de máximo alcance y el valor de éste

- Para una pared vertical β = π / 2 y resulta

- que quiere decir que, lógicamente, debemos lanzar el proyectil en vertical y el alcance será la máxima altura correspondiente a un tiro vertical
Para el caso particular β = π / 6
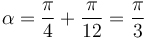
es decir, que se alcanza la distancia máxima para un ángulo de 60º respecto a la horizontal (y de 30º respecto al plano).
Si sustituimos los datos de la aceleración de la gravedad y la rapidez inicial
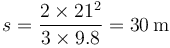
4 Caso particular
El caso particular α = π / 3 es justamente el que produce el alcance máximo, según acabamos de ver, aunque esto no es necesario para lo que sigue.
4.1 Rapidez de impacto
El tiempo que tarda el proyectil en impactar lo obtenemos de las ecuaciones anteriores
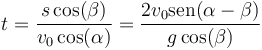
que para los ángulos indicados vale
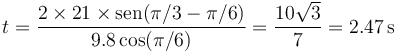
Para todo instante t, la velocidad de la partícula es
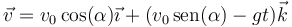
y en el instante de impacto, sustituyendo el valor del tiempo,

Sustituimos los valores de los ángulos
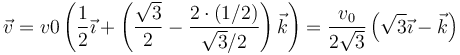
El módulo de este vector es

que para el valor dado de la velocidad inicial da
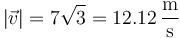
4.2 Componentes intrínsecas de la aceleración
La aceleración, como vector, es la misma en todo el moviminto:
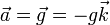
sin embargo, sus componentes intrínsecas van cambiando, ya que la velocidad va cambiando de dirección.
En el momento del impacto, el vector tangente a la trayectoria es, para los ángulos del problema
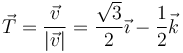
La aceleración tangencial (escalar) es la proyección de la aceleración sobre este vector
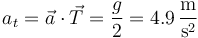
y en forma vectorial

La aceleración normal es la diferencia vectorial entre la completa y la tangencial
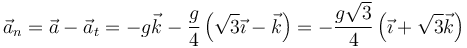
siendo su módulo
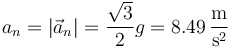
4.3 Variación de la energía
El cálculo de la energía corresponde al tema “Energía y leyes de conservación”, aunque en este caso se piden solamente fórmulas muy conocidas.
La variación en la energía cinética es

y la de la energía potencial
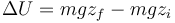
siendo la masa del proyectil
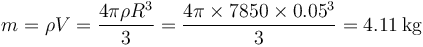
Esto nos da una variación en la energía cinética
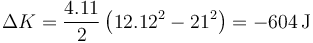
y en la energía potencial
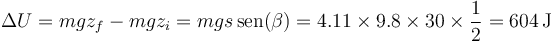
Puesto que se conserva la energía mecánica, la ganancia en energía potencial coincide con la disminución en la cinética.





