Estática del sólido rígido
De Laplace
Contenido |
1 Introducción. Ecuaciones de la estática
La estática del sólido (y de los sistemas de sólidos) es el estudio de las condiciones en que un sólido o sistema permanece en reposo. Matemáticamente la expresión de la condición de equilibrio es muy simple. Puesto que se anulan tanto la aceleración del centro de masas como la aceleración angular del sólido, se cumple que
Como consecuencia de esto, también se anula el momento de las fuerzas respecto a cualquier otro punto
Sin embargo, la aplicación práctica de estas ecuaciones es mucho más complicada, ya que a menudo una o varias de las fuerzas que actúan sobre el sólido son fuerzas de reacción vincular, cuyo valor es desconocido a priori y que son incógnitas adicionales del problema. Normalmente, un problema de estática de sólidos se compone de varios elementos:
- Determinación de la(s) posición(es) de equilibrio posibles, si existen.
- Cálculo de las fuerzas y pares de reacción vincular.
En la determinación de la posición de equilibrio simplifica mucho la tarea el elegir un centro de reducción O adecuado respecto al cual calcular el momento de las fuerzas. En particular, para el contacto puntual de dos sólidos, suele ser lo más conveniente el elegir como centro de reducción el punto de contacto, ya que de esta forma se anula el momento de las fuerzas de reacción aplicadas en él.
Adicionalmente, suele existir una parte que requiere el estudio de la energía del sistema y del comportamiento de éste cuando se somete a una perturbación:
- Determinación de la estabilidad de los puntos de equilibrio.
Como ejemplo sencillo, tenemos el estudio del equilibrio de una barra apoyada en el suelo y en una pared.
2 Teorema de Varignon
De entre los diferentes teoremas aplicables para la determinación de las condiciones de equilibrio, existe uno de especial utilidad, especialmente en el caso de figuras planas, ya que facilita la solución por métodos geométricos.
- Dadas varias fuerzas concurrentes el momento resultante de las distintas fuerzas es igual al momento de la resultante de ellas aplicada en el punto de concurrencia.
Donde entendemos como fuerzas concurrentes aquellas cuyas rectas soporte (que pasan por el punto de aplicación y llevan la dirección de la fuerza) se cortan en un punto O.
La demostración es la siguiente: tenemos n fuerzas concurrentes,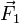 
, 
,... 
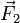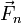, aplicadas en los puntos A1 < math > , < math > A2,... An. El momento resultante respecto a un punto O es
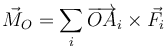
Ahora bien, por pasar cada recta soporte por el punto de concurrencia P se cumple para cada una
por ser vectores paralelos. Por tanto, para cada momento individual
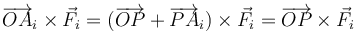
y para la resultante
Por tanto, el procedimiento para hallar el momento resultante consiste en llevar todas las fuerzas al punto de concurrencia, hallar la resultante de todas las fuerzas y luego calcular su momento respecto al punto O.
2.1 Teorema de las tres fuerzas
Un corolario de este teorema es que dado que la resultante de las fuerzas debe anularse, la condición para que un sólido sometido a tres fuerzas esté en equilibrio es que exista un punto P tal que las rectas soporte pasen por él. De esta forma se anulan simultáneamente la resultante de las fuerzas y la de los momentos. Si este punto no existe, el sólido no puede estar en equilibrio.
3 Ejemplos de estática del sólido
Dentro de las múltiples aplicaciones de la estática, hay varias ilustradas en los problemas de la asignatura:
- Las diferentes fuerzas de reacción de una mesa apoyada en dos caballetes
- El posible equilibrio de una barra apoyada en una pared
