Potencial eléctrico de un segmento cargado

De Laplace

Revisión a fecha de 19:14 30 nov 2008; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución
- 2.1 Potencial eléctrico
- 2.2 Superficies equipotenciales

1 Enunciado

Sea un segmento rectilíneo de longitud $L$ , sobre el cual existe una densidad de carga uniforme $λ$ .

Halle el potencial que produce en un punto cualquiera del espacio.
Demuestre que las equipotenciales son elipsoides con focos los extremos del segmento.

2 Solución

2.1 Potencial eléctrico

El cálculo del potencial eléctrico debido a un segmento es algo más complicado que el del campo eléctrico, pese a que la integral es aparentemente más simple. Para hallar el potencial por integración directa, debemos resolver la integral

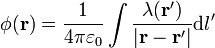
$\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \frac{\lambda(\mathbf{r'})}{|\mathbf{r}-\mathbf{r}'|}\mathrm{d}l'$

En nuestro caso, empleando los mismos ejes y las mismas variables que para el cálculo del campo eléctrico, nos queda

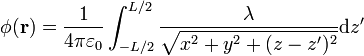
$\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int_{-L/2}^{L/2} \frac{\lambda}{\sqrt{x^2+y^2+(z-z')^2}}\mathrm{d}z'$

Empleando de nuevo el cambio de variable

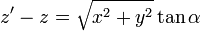
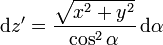
$z'-z=\sqrt{x^2+y^2}\tan\alpha$ $\mathrm{d}z'=\frac{\sqrt{x^2+y^2}}{\cos^2\alpha}\,\mathrm{d}\alpha$

nos queda ahora

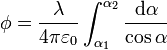
$\phi= \frac{\lambda}{4\pi\varepsilon_0}\int_{\alpha_1}^{\alpha_2}\frac{\mathrm{d}\alpha}{\cos\alpha}$

Esta integral no es inmediata, pero existen técnicas “mecánicas” para resolverla. Una posibilidad es introducir el nuevo cambio de variable

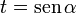
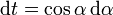
$t = \mathrm{sen}\,\alpha$ $\mathrm{d}t = \cos\alpha\,\mathrm{d}\alpha$

y la integral se nos transforma en

$\phi = \frac{\lambda}{4\pi\varepsilon_0}\int_{t_1}^{t_2}\frac{\mathrm{d}t}{1-t^2}$

Esta integral se descompone en dos fracciones y obtenemos finalmente

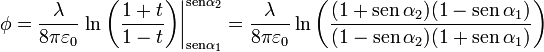
$\phi = \frac{\lambda}{8\pi\varepsilon_0}\left.\ln\left(\frac{1+t}{1-t}\right)\right|_{\mathrm{sen}\alpha_1}^{\mathrm{sen}\alpha_2} = \frac{\lambda}{8\pi\varepsilon_0}\ln\left(\frac{(1+\mathrm{sen}\,\alpha_2)(1-\mathrm{sen}\,\alpha_1)}{(1-\mathrm{sen}\,\alpha_2)(1+\mathrm{sen}\,\alpha_1)}\right)$

Una forma alternativa y mucho más directa consiste en emplear funciones hiperbólicas. Si en lugar del cambio de variable de la tangente, empleamos

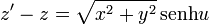
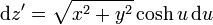
$z'-z=\sqrt{x^2+y^2}\,\mathrm{senh}u$ $\mathrm{d}z'=\sqrt{x^2+y^2}\cosh u\,\mathrm{d}u$

nos queda, simplemente,

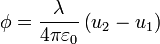
$\phi = \frac{\lambda}{4\pi\varepsilon_0}\left(u_2-u_1\right)$

o, en términos de las dimensiones del segmento,

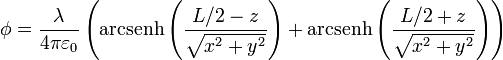
$\phi = \frac{\lambda}{4\pi\varepsilon_0}\left(\mathrm{arcsenh}\left(\frac{L/2-z}{\sqrt{x^2+y^2}}\right)+\mathrm{arcsenh}\left(\frac{L/2+z}{\sqrt{x^2+y^2}}\right)\right)$

2.2 Superficies equipotenciales

Se trata de ver que la fea ecuación, en cilíndricas,

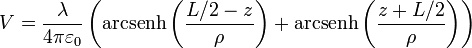
$V = \frac{\lambda}{4\pi\varepsilon_0}\left(\mathrm{arcsenh}\left(\frac{L/2-z}{\rho}\right)+\mathrm{arcsenh}\left(\frac{z+L/2}{\rho}\right)\right)$

para un $V$ fijo, es la de un elipsoide en torno al segmento

Antes de hacer el cálculo veamos que este resultado es razonable. Para el caso de una carga puntual tenemos equipotenciales esféricas. Para un segmento obtenido estirando una carga a lo largo de una línea, las superficies equipotenciales, que envuelven a la carga, deberían ser al menos superficies parecidas a elipsoides.

Vamos con la demostración. Comenzamos despejando uno de los arcosenos

$\frac{z-L/2}{\rho} = \mathrm{senh}\left(\mathrm{arcsenh}\left(\frac{z+L/2}{\rho}\right)-K\right)$ $\left(K \equiv \frac{4\pi\varepsilon_0V}{\lambda}\right)$

Desarrollando ahora el seno de la suma

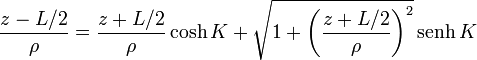
$\frac{z-L/2}{\rho} = \frac{z+L/2}{\rho}\cosh K+ \sqrt{1+\left(\frac{z+L/2}{\rho}\right)^2}\,\mathrm{senh}\,K$

Despejando ahora la raíz y multiplicando por $ρ 2$ nos queda

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): z\left(1+\cosh K) + \frac{L}{2}(\cosh K-1) \sqrt{\rho^2+(z+L/2)^2}\,\mathrm{senh}\,K

Aplicando las fórmulas del ángulo doble

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): z \cosh^2\left(\frac{K}}{2}\right) + \frac{L}{2}\mathrm{senh}^2\left(\frac{K}}{2}\right) = \sqrt{\rho^2+(z+L/2)^2}\,\cosh^2\cosh\left(\frac{K}}{2}\right)\mathrm{senh}\left(\frac{K}}{2}\right)

Potencial eléctrico de un segmento cargado

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Potencial eléctrico

2.2 Superficies equipotenciales

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES