Integración aproximada de la velocidad
De Laplace
Revisión a fecha de 17:28 1 nov 2013; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
Una partícula se mueve a lo largo de una recta, siendo su velocidad (en el SI) como función del tiempo, la dada por la gráfica
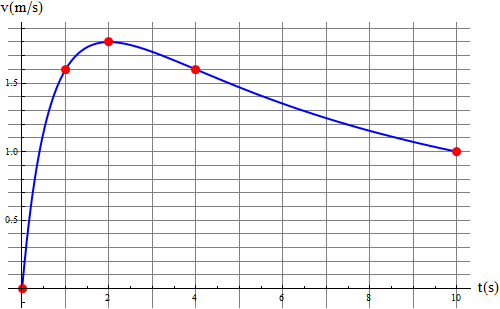
La partícula parte de x = 0.
- Aprovechando los puntos en que la curva cruza la cuadrícula, calcule aproximadamente la posición en que se encontrará la partícula en
.
- Calcule el valor exacto de esta posición, sabiendo que la ley para la velocidad, en el SI, es
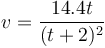
- ¿Cuál es el error relativo cometido en el apartado anterior?
- Con ayuda de la cuadrícula halle el valor aproximado de la aceleración en
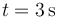. Calcule el valor exacto y el error cometido con la aproximación.
2 Integración numérica
El área bajo la curva se puede aproximar mediante el método de los trapecios. Para ello, a partir de una serie de puntos conocidos de la curva, trazamos los trapecios que definen con el eje.
Si la curra pasa por los puntos (tn,vn) y (tn + 1,vn + 1), el área de cada trapecio es la altura multiplicada por la media entre las dos bases. Este área equivale, aproximadamente, al desplazamiento entre esos dos instantes
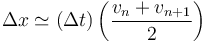
Aplicando esto a nuestro caso, tenemos los puntos señalados
| header 1 | header 2 | header 3 |
|---|---|---|
| row 1, cell 1 | row 1, cell 2 | row 1, cell 3 |
| row 2, cell 1 | row 2, cell 2 | row 2, cell 3 |
