Energía de esferas concéntricas

De Laplace

Contenido 1 Enunciado 2 Solución 2.1 Energía de una superficie esférica 2.2 Energía de dos esferas concéntricas

1 Enunciado

Halle la energía electrostática almacenada en una superficie esférica de radio a, que almacena una carga Q, distribuida uniformemente sobre ella.

Calcule la energía electrostática almacenada en un sistema de dos superficies esféricas concéntricas de radios a y b, cargadas, respectivamente con cargas + Q y − Q, distribuidas uniformemente.

¿Se verifica el principio de superposición, esto es, es la energía de las dos esferas la suma de las energías de cada esfera por separado?

2 Solución

2.1 Energía de una superficie esférica

La energía electrostática de una distribución de carga superficial viene dada por

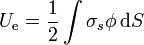
siendo el potencial en los puntos en que se encuentran las cargas. En el caso de una superficie esférica cargada uniformemente, Potencial_en_el_centro_de_una_esfera#A_partir_del_campo_el.C3.A9ctricoel potencial que crea en todos los puntos del espacio es

En los puntos de la superficie esférica r = a vale tanto la expresión interior como la exterior por ser el potencial una función continua

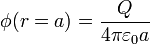
y por ello la energía electrostática almacenada por la esfera es

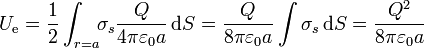
dado que el potencial tiene el mismo valor en todos los puntos de la superficie, puede salir de la integral. El resultado es una función cuadrática de la carga. Esto quiere decir que, tanto si la superficie esférica esta cargada positivamente, como si lo está negativamente, la energía es siempre positiva.

2.2 Energía de dos esferas concéntricas