Expansión lineal de un gas

De Laplace

Revisión a fecha de 23:45 21 feb 2013; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Temperatura final
3 Variación de la energía interna
4 Trabajo realizado
5 Calor que entra en el gas

1 Enunciado

Se tiene una cantidad fija de un gas ideal diatómico situada a una presión $p 0$ , volumen $V 0$ y temperatura $T 0$ . Experimenta un proceso tal que la presión final es $2 p 0$ y el volumen $2 V 0$ .

En este proceso, ¿cómo varía la temperatura?
Halle el incremento de la energía interna en este proceso

Supongamos que el proceso anterior ocurre de manera cuasiestática según la ley

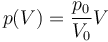
$p(V) = \frac{p_0}{V_0}V$

¿Cuánto trabajo se realiza sobre el gas en esta expansión cuasiestática?
¿Cuánto calor entra en el gas en la expansión cuasiestática?

2 Temperatura final

Puesto que la cantidad de gas es constante, podemos emplear la ley de los gases ideales en la forma

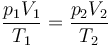
$\frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}$

donde en este caso

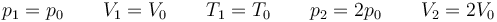
$p_1=p_0\qquad V_1=V_0\qquad T_1 = T_0\qquad p_2=2p_0\qquad V_2=2V_0$

lo que nos da

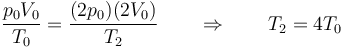
$\frac{p_0V_0}{T_0}=\frac{(2p_0)(2V_0)}{T_2}\qquad\Rightarrow\qquad T_2 = 4T_0$

Vemos que en este proceso aumentan simultáneamente la presión, el volumen y la temperatura. Una expansión no significa necesariamente una reducción en la presión, ya que simultáneamente se puede estar calentando el gas y aumentando su presión y temperatura.

3 Variación de la energía interna

La energía interna de un gas ideal solo depende de la temperatura. Si la capacidad calorífica es constante, la energía interna se puede escribir

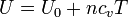
$U = U_0+n c_v T\,$

siendo su incremento

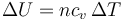
$\Delta U = n c_v\,\Delta T$

Podemos relacionar esto con los datos del problema observando que

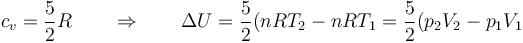
$c_v = \frac{5}{2}R\qquad\Rightarrow\qquad \Delta U = \frac{5}{2}(nRT_2-nRT_1=\frac{5}{2}(p_2V_2-p_1V_1$

Sustituyendo las presiones y volúmenes

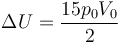
$\Delta U = \frac{15p_0V_0}{2}$

4 Trabajo realizado

En un proceso cuasistático puede calcularse el trabajo neto realizado sobre un sistema mediante la integral

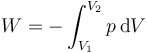
$W = -\int_{V_1}^{V_2}p\,\mathrm{d}V$

Para este caso en concreto

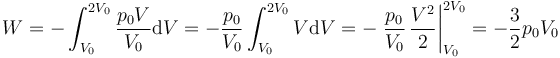
$W = -\int_{V_0}^{2V_0}\frac{p_0V}{V_0}\mathrm{d}V=-\frac{p_0}{V_0}\int_{V_0}^{2V_0}V\mathrm{d}V = -\left.\frac{p_0}{V_0}\,\frac{V^2}{2}\right|_{V_0}^{2V_0}=-\frac{3}{2}p_0V_0$

El trabajo es negativo pué al expandirse, realmente es el gas interior el que realiza trabajo sobre el ambiente.

5 Calor que entra en el gas

Una vez que tenemos el trabajo y la variación de la energía interna, el cálculo del calor que entra es inmediato, por aplicación del principio de la termodinámica

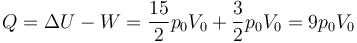
$Q = \Delta U - W = \frac{15}{2}p_0V_0+\frac{3}{2}p_0V_0 = 9p_0V_0$

Este calor que entra es responsable tanto del aumento de la energía interna como del trabajo realizado por el gas sobre el ambiente.

Expansión lineal de un gas

De Laplace

Contenido

1 Enunciado

2 Temperatura final

3 Variación de la energía interna

4 Trabajo realizado

5 Calor que entra en el gas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES