Corriente eléctrica (GIE)
De Laplace
Contenido |
1 Introducción
La electrostática es el estudio del campo y las fuerzas debidos a cargas en reposo. Sin embargo, no es ese el estado natural de las cargas. Éstas suelen encontrarse en movimiento, bien debido a la agitación térmica, bien impulsadas por campos eléctricos y magnéticos. Cuando tenemos un movimiento colectivo de cargas se dice que tenemos una corriente eléctrica.
Si la corriente es independiente del tiempo se denomina corriente continua o corriente estacionaria. En caso contrario es una corriente dependiente del tiempo (con la corriente alterna como caso particular).
En situaciones donde hay corrientes eléctricas, aunque sean estacionarias, ya dejan de ser ciertas algunas de las propiedades de la electrostática. En particular, la afirmación de que es nulo el campo eléctrico en el interior de un conductor ya no es cierta. Eso solo vale en el equilibrio electrostático. Si hay corrientes es porque las cargas se ven impusladas por alguna fuerza y en la mayoría de los casos esa fuerza es debida a la presencia de un campo eléctrico en el interior del material.
2 Modelos de conducción
Las corrientes eléctricas tienen todas en común el movimiento de cargas por el vacío o el interior de un material, pero el mecanismo por el que esto ocurre es muy diverso. Para describirlos se usan los modelos de conducción, que tienen una parte cualitativa y una descripción matemática (que no consideraremos).
- Disoluciones salinas
- El caso más sencillo es el de una cantidad de agua en el que hay sales disueltas. En este caso, flotando en la sopa hay iones de diferentes cargas y signos. De entrada tenemos los iones OH− y H+ en que se disocia el agua, pero además tenemos Cl−, Na+, Ca2+, K+, etc. dependiendo de las sales que haya disueltas. Cada una de las variedades cargadas se denomina una especie de portadores de carga, caracterizada por una valencia Z. Por ejemplo, todos los iones Cl− constituyen una especie de valencia Z = − 1, todos los iones Ca2+ forman una especie de valencia Z = + 2. En agua destilada tenemos dos especies de portadores de carga (OH− y H+). Si tiene sal común, habrá 4 especies (Cl−, Na+, OH− y H+). En el agua de mar hay una enorme variedad de especies.
- Conductores metálicos
- Constituyen el caso más típico de conductores y son los de mayores aplicaciones industriales, donde se usan materiales conductores como cobre, oro, platino, etc. En un material metálico la conducción se produce porque hay electrones libres. Existe una red de iones fijos (los núcleos y la mayoría de los electrones de cada átomo) y una nube de electrones formada por uno o dos electrones por cada átomo (uno en el caso del cobre). Estos electrones no están asociados a ningún átomo en concreto, sino que pertenecen conjuntamente a toda la red, produciendo lo que se llama un enlace metálico. Estos electrones pueden moverse más o menos libremente por el interior del material, formando la corriente eléctrica. En este caso tenemos una sola especie de portadores de carga, los electrones.
- Semiconductor
- Un semiconductor, como el carbono o el silicio, está formado por una red cristalina en la que los electrones están ligados a cada átomo formando enlaces covalentes. En una red sin defectos y a 0K no puede haber corriente eléctrica ya que no hay portadores de carga disponibles.

- Sin embargo, existen dos motivos por los que aparecen portadores en estos materiales:
- Por la agitación térmica, que hace que algunos electrones tengan energía suficiente para abandonar el átomo al que pertenecen.
- Por la presencia de impurezas (“dopado”) de otros materiales, que tienen un electrón de más o de menos.


- En ambos casos, tenemos un cierto número de electrones que pueden moverse por la red, funcionando como portadores de carga. Pero además, el efecto de que un electrón abandone su átomo es la aparición de un hueco. A medida que otros electrones van ocupando este hueco, el efecto es el movimiento aparente del hueco en sentido contrario. Por ello, en un semiconductor tenemos dos especies de portadores: los electrones, con valencia −1 y los huecos con valencia +1.
- Plasma
- Un plasma es un estado de la materia consistente en un gas ionizado. En un plasma tenemos una gran variedad de portadores, ya que hay gran número de estados de ionización posible. En un plasma las cargas se mueven por el aire sometidas a las interacciones con el resto de cargas y con los campos externos.
3 Densidad de corriente
La magnitud que mide el movimiento promedio de las cargas en un material es la densidad de corriente. Para definirla se toma un elemento de volumen Δv (que es microscópico, pero contiene millones de cargas en su interior), situado en el punto  , y se calcula el promedio del producto de las cargas por la velocidad
, y se calcula el promedio del producto de las cargas por la velocidad
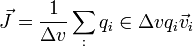
La densidad de corriente es una magnitud vectorial, análoga hasta cierto punto a la cantidad de movimiento: cuanta más carga haya, mayor es la densidad de corriente; cuanto más rápida se mueva, mayor en la densidad. Si no hay cargas (vacío) o no se mueven (electrostática) la densidad de corriente se anula.
De la definición de la densidad se tiene que se mueve en C·(m/s)/m³ = A/m² donde un amperio (A) es igual a 1 C·s.
Puesto que en la expresión aparece la velocidad, el sumatorio se puede restringir a los portadores de carga, ya que las cargas estáticas no contribuyen.
Por otro lado, podemos hacer la aproximación de que todos los iones de la especie k se mueven con la misma velocidad promedio. En ese caso, podemos agrupar términos y escribir la densidad de corriente como
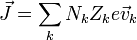
donde
- La suma se hace sobre el número de especies (una en un conductor metálico, dos en un semiconductor, unas cuantas en una disolución).
- Nk es la densidad numérica del portador k (p.ej. cuantos electrones libres hay por unidad de volumen).
- Zk, es la valencia de la especie k, que sería -1 para los electrones.
- e es la carga elemental, que vale aproximadamente
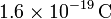 .
.
-
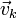 es la velocidad promedio de los iones de la especie k. A esta velocidad se la conoce como velocidad de arrastre.
es la velocidad promedio de los iones de la especie k. A esta velocidad se la conoce como velocidad de arrastre.
En el caso de un conductor metálico, los únicos portadores son los electrones y al expresión anterior se reduce a
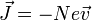
siendo N la densidad de electrones libres (no de todos los electrones, los que están fijos en los átomos no cuentan) y  es la velocidad de arrastre. Vemos que en este caso concreto, los electrones se mueven en un sentido y la densidad de corriente va en sentido contrario, por ser la carga negativa. Esto es fuente de infinitas confusiones. Por ello, a la hora de describir el movimiento de las cargas en un conductor, es preferible suponer que las cargas que se mueven son las positivas, aunque no corresponda a lo que ocurre en realidad. Los cálculos también son correctos de esta forma y es más sencillo.
es la velocidad de arrastre. Vemos que en este caso concreto, los electrones se mueven en un sentido y la densidad de corriente va en sentido contrario, por ser la carga negativa. Esto es fuente de infinitas confusiones. Por ello, a la hora de describir el movimiento de las cargas en un conductor, es preferible suponer que las cargas que se mueven son las positivas, aunque no corresponda a lo que ocurre en realidad. Los cálculos también son correctos de esta forma y es más sencillo.
El valor de la velocidad de arrastre puede ser extremadamente pequeño. Para un hilo de cobre que soporta una densidad de corriente de 1 A/mm² no llega a 1 mm/s. Uno pensaría que los electrones se mueven mucho más rápido y así es para cada electrón. La velocidad de arrastre es la velocidad promedio, no la rapidez promedio. Aunque el electrón puede moverse con una rapidez próxima a la velocidad de la luz, la mayor parte se su movimiento es aleatorio y hay muy poco avance neto.
La presencia de una densidad de corriente en un punto no es incompatible con la ausencia de una densidad de carga en ese punto. De hecho, podemos tener los cuatro casos:
- Densidad de carga nula ρ = 0 y densidad de corriente nula
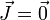
- Esto es lo que ocurre en un vacío total, en el que no hay nada, pero también en el interior de un conductor en equilibrio. En ese caso, que no haya densidad de carga no significa que no haya cargas. Hay millones de ellas, lo que ocurre es que hay tantas positivas como negativas. Al estar en equilibrio, en promedio están inmóviles y también se anula la densidad de corriente.
- Densidad de carga no nula
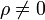 y densidad de corriente nula
y densidad de corriente nula 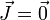
- Es lo que ocurre cuando tenemos una densidad de carga estática, como en muchos problemas de electrostática.
- Densidad de carga nula ρ = 0 y densidad de corriente no nula
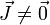
- Es el caso habitual en un material conductor (metal, disolución o semiconductor). En cada punto hay tantas cargas positivas como negativas, pero se están moviendo. En un metal, por cada electrón en movimiento hay un ion en reposo. Solo los primeros contribuyen a la densidad de corriente, pero los dos lo hacen a la densidad de carga.
- Densidad de carga no nula
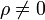 y densidad de corriente no nula
y densidad de corriente no nula 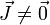
- Es el caso general, que se da sobre todo en los plasmas, en los que tenemos nubes de cargas en movimiento, sin que estén compensadas las positivas por las negativas.
4 Intensidad de corriente
La densidad de corriente es una medida adecuada de lo que ocurre en cada punto de un material, de si las cargas se están moviendo o no y hacia adonde lo hacen.
En la mayoría de las aplicaciones, en particular en la teoría de circuitos, interesa más el efecto global del movimiento de las cargas.
Supongamos que tenemos un material conductor en forma de cilindro (un cable, por ejemplo) por el cual está circulando una corriente. Nos preguntamos entonces cuanta carga atraviesa una sección del conductor en la unidad de tiempo. Esta cantidad es la intensidad de corriente definida como el flujo de la densidad de corriente través de una sección del conductor
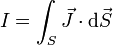
de forma que la carga que pasa en un tiempo dt es igual a
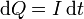
La intensidad de corriente es una magnitud escalar con signo. El signo de la intensidad de corriente nos dice para donde va la corriente respecto de la orientación de la superficie. Cuando se traza la superficie S, su vector normal tiene dos posibles sentidos. Si al hallar el flujo resulta una cantidad positiva quiere decir que las cargas positivas se mueven en el sentido elegido. Si la intensidad resulta negativa, quiere decir que se mueven en el sentido contrario al elegido (con las cargas negativas sería al revés).
La unidad de medida de la intensidad de corriente es el amperio (A), que es una de las unidades fundamentales del Sistema Internacional. Un amperio es una medida razonable para las corrientes existentes en la industria. Un aparato electrónico, como un ordenador tiene corrientes del orden de los mA. Una red eléctrica doméstica o una máquina puede tener corrientes de varios amperios. Una red de alta tensión puede llegar hasta los kA circulando por los cables.
5 Ley de conservación de la carga
Una de las propiedades fundamentales de la interacción eléctrica es que la carga eléctrica se conserva. Para cualquier volumen la cantidad de carga contenida en su interior solo puede cambiar porque entre carga desde fuera porque salga al exterior, nunca porque se cree de la nada.
Matemáticamente se expresa de la siguiente forma:
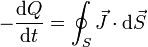
donde:
- S es una superficie cerrada que contiene un volumen v.
- Q = Q(t) es la carga contenida en v
- dQ / dt es el aumento de la carga contenida por unidad de tiempo.
- − dQ / dt es la disminución de la carga contenida por unidad de tiempo.
-
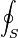 representa la integral sobre toda la superficie cerrada S.
representa la integral sobre toda la superficie cerrada S.
-
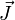 es la densidad de corriente en todos los puntos de la superficie S
es la densidad de corriente en todos los puntos de la superficie S
-
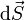 es el vector diferencial de superficie
es el vector diferencial de superficie
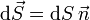
- donde para una superficie cerrada,
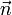 se toma siempre hacia el exterior.
se toma siempre hacia el exterior.
Esta misma ley puede leerse de otras formas. Por ejemplo si la escribimos
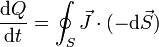
diríamos que lo que aumenta la carga contenida se debe al flujo de corriente hacia el interior.
- Caso de una corriente estacionaria
- En el estado estacionario, la carga contenida en un volumen no cambia, por lo que la ley de conservación de la carga se reduce a
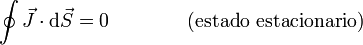
5.1 Aplicación a un circuito
5.1.1 Conservación de la corriente
La ley de conservación de la carga tiene una aplicación inmediata a la teoría de circuitos. Consideremos en primer lugar el caso de un conductor a lo largo del cual circula una corriente, siendo el exterior vacío (que suponemos perfectamente aislante). El conductor puede tener sección variable y estar hecho de diferentes materiales.
Suponemos que por este conductor circula una corriente estacionaria.
Si consideramos una superficie cerrada S que corta al conductor en dos secciones S1 y S2. Por ser la corriente estacionaria
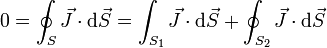
Si tomamos la intensidad de corriente a lo largo del conductor como el flujo de la densidad de corriente hacia adelante, entonces

(el signo negativo de la primera integral se debe a la diferente orientación del vector normal). Tenemos entonces que

lo cual expresa una propiedad bastante intuitiva: por un conductor por el que circula una corriente estacionaria, la intensidad de corriente es la misma para cualquier sección que tomemos, o dicho en términos aun más llanos, que todas las cargas que entran por un sitio deben salir por el otro.
En términos de teoría de circuitos esto implica que:
- Dado un conjunto de elementos puestos en serie, la intensidad de corriente es la misma en todos ellos.
En el caso de un conductor de sección variable, se deduce que la densidad de corriente es mayor donde la sección es menor y viceversa.
5.1.2 Ley de Kirchhoff para los nodos
Lo anterior vale para el caso de que la corriente fluya a lo largo de una sola rama. ¿qué ocurre si tenemos varias ramas conectadas en un nodo de un circuito? En ese caso, el razonamiento es una extensión del anterior. Considerando una superficie cerrada alrededor del nodo, que cortará a las diferentes ramas en las secciones en las superficies S1, S2,… Sn. Al ser nula la integral sobre la superficie cerrada obtenemos
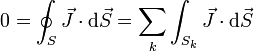
o, en términos de las intensidades de corriente
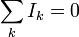
donde consideramos todas las corrientes como saliendo del nodo (lógicamente, algunas serán positivas y otras negativas). Esta es la conocida como ley de Kirchhoff para los nodos (o primera ley de Kirchhoff).
Si distinguimos las corrientes que llegan al nodo y las que salen de él con su signo correspondiente, queda
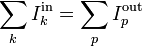
es decir, que la suma de las corrientes que llegan al nodo es igual a la suma de las que salen de él. De nuevo, esta es una propiedad intuitiva. Si a un nodo llega una corriente I0 y del nodo salen dos ramas, la corriente se repartirá entre ambas, de forma que
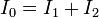
En particular, este resultado nos dice que dada una asociación de elementos en paralelo, la intensidad corriente total que circula por la asociación es la suma de las que van por cada una de las ramas.
6 Ley de Ohm
En los apartados anteriores hemos descrito el movimiento de las cargas, sin atender a las causas que lo producen. Para tener en cuenta las causas necesitaríamos o bien medir experimentalmente la corriente como función de otros parámetros, o bien analizar los diferentes modelos de conducción, para ver qué relación teórica hay entre la densidad de corriente y el campo eléctrico (y otras fuerzas aplicadas).
El resultado es que en la gran mayoría de las materiales existe una relación sencilla entre la densidad de corriente y el campo eléctrico en el interior del material. Esta relación es la ley de Ohm:
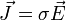
donde σ es una propiedad de cada material conocida como su conductividad. Se mide en el SI en siemens/metro (S/m) y es la propiedad física que más cambia de unas sustancias a otras.
| Material | σ (S/m) | ρ (Ω·m) |
|---|---|---|
| Plata | 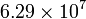
| 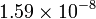
|
| Cobre | 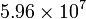
| 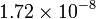
|
| Oro | 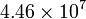
| 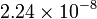
|
| Hierro | 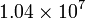
| 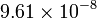
|
| Agua de mar | 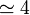
| 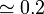
|
| Agua destilada | 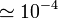
| 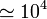
|
| Goma | 10 − 15 − 10 − 13 | 1013 − 1015 |
A menudo se da como dato la inversa de la conductividad, llamada la resistividad (ρ o r), que se mide en Ω·m.
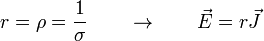
La ley de Ohm nos dice sencillamente que si las cargas se mueven es porque hay un campo eléctrico que las empuja, aunque debido a la fricción con el material, no es la aceleración, sino la velocidad, la que es proporcional al campo eléctrico.
La ley de Ohm no es una ley universal. Solo se cumple en los llamados materiales óhmicos (que son la mayoría) pero no, por ejemplo, en los plasmas.
La excepción más importante de sistema en el que no se cumple la ley de Ohm es en un generador. Como veremos, en un generador la densidad de corriente va en sentido contrario al campo eléctrico, lo cual es la negación absoluta de la ley de Ohm.
6.1 Aplicación a un conductor filiforme
La ley de Ohm así enunciada no es como suele aparecer en los libros de teoría de circuitos. La razón es que al analizar un circuito no interesa tanto lo que ocurre en cada elemento de volumen, y sílo que ocurre a nivel macroscópico, mediante magnitudes medibles de forma sencilla como la intensidad de corriente y la diferencia de potencial.
Para llegar a la ley de Ohm tal como se ve en teoría de circuitos consideramos en primer lugar el caso de un conductor filiforme (un hilo), que es aquél que tiene una longitud mucho mayor que su diámetro y que su radio de curvatura. Este hilo va de un punto A a un punto B, siguiendo una cierta curva (no tiene por qué ser una recta). Suponemos que la intensidad de corriente fluye de A a B. Nos preguntamos por la diferencia de potencial entre los dos extremos. Por definición de d.d.p. tenemos que

Puesto que en el cable se cumple la ley de Ohm
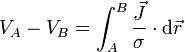
Al recorrer la curva que constituye un conductor filiforme el desplazamiento va en la dirección del vector tangente
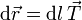
Por otro lado, por ser muy estrecho, la densidad de corriente va también en el sentido longitudinal
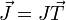
lo que nos deja la d.d.p como la integral escalar
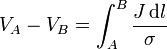
En el caso de un conductor filiforme se cumple además que la densidad de corriente es la misma en todos los puntos de una sección transversal, de forma que podemos hacer la aproximación
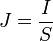
siendo I la intensidad de corriente que circula por el cable. Esta intensidad es la misma a lo largo de todo él, por lo que podemos sacarla de la integral y nos queda finalmente
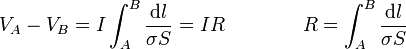
La cantidad R es la resistencia eléctrica del hilo. Es una integral porque, en principio, la conductividad y la sección pueden ir variando a lo largo del cable. En el caso común de un cable de un solo material con sección constante

7 Resistencia eléctrica
Acabamos de ver que en un cable hecho de un material óhmico se cumple una relación de proporcionalidad entre la diferencia de potencial entre sus extremos y la intensidad de corriente que circula por el cable

Esta es la llamada ley de Ohm en la teoría de circuitos y es generalizable a gran variedad de situaciones aunque no tengamos un hilo. Siempre que haya dos electrodos entre los cuales se encuentra un material (o materiales) óhmicos, se cumple esta misma relación, aunque el valor de la resistencia será una función complicada de la geometría y los materiales interpuestos.
La resistencia eléctrica se mide en ohmios (Ω) definidos como
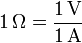
La ley de Ohm circuital también puede escribirse
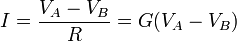
donde G = 1/R es la conductancia del sistema, medida en siemens (S)
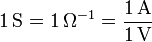
En las expresiones anteriores, para que salgan los signos correctos, si se halla la diferencia de potencial entre A y B, hay que suponer que la corriente va de A a B (si se da la vuelta a ambas magnitudes, sigue saliendo el resultado correcto, pero si solo se la da la vuelta a una resulta el signo incorrecto.
Un elemento de circuito caracterizado por poseer una resistencia eléctrica se denomina un resistor (del mismo modo que uno que tiene capacidad es un condensador), aunque se usa a menudo la palabra resistencia tanto para el dispositivo como para su propiedad. Su símbolo es una línea quebrada o un rectángulo.
7.1 Asociaciones de resistencias
De manera análoga a los condensadores, los resistores pueden combinarse para formar un circuito con múltiples elementos. Como con los condensadores tenemos dos casos particulares:
- Resistencias en serie
- cuando no hay ninguna derivación en el punto de conexión, de manera que toda la corriente que pasa por una pasa por la otra
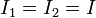
- La diferencia de potencial de la asociación es la suma de las individuales. Si A y B son los extremos y C es el punto de conexión
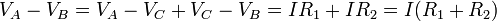
- por lo que la resistencia equivalente a una asociación en serie de dos resistores es la suma de las resistencias individuales
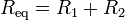
- Resistencias en paralelo
- cuando se encuentran conectadas por sus dos extremos A y B de forma que la d.d.p. en ambos resistores es la misma
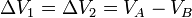
- La corriente que llega a la asociación es en este caso la suma de las dos individuales
![\frac{\Delta V}{R_\mathrm{eq}}=I= I_1 + I_2 = \frac{\Delta V}{R_1}]+\frac{\Delta V}{R_2}=\left(\frac{1}{R_1}+\frac{1}{R_2}\right)\Delta V](/wiki/images/math/2/7/4/27437ea96654a8f8ee17c9111f84764b.png)
- En una asociación en paralelo la conductancia equivalente es la suma de las conductancias individuales

8 Potencia eléctrica. Efecto Joule
La transmisión de una corriente eléctrica implica un consumo de energía.
Imaginemos un sistema (no necesariamente óhmico) con dos extremos A y B, situados a potenciales VA y VB. Si una carga dQ entra por A y la misma carga sale por B, se ha realizado un trabajo sobre el sistema igual al producto de la carga por la diferencia de potencial

La carga que atraviesa el sistema es proporcional a la intensidad de corriente

La potencias desarrollada sobre el sistema (el flujo de trabajo hacia el interior) será igual a

Si consideramos la potencia desarrollada por el sistema sobre el entorno

(suponemos en todo momento que la corriente va de A a B).
Este resultado es bastante general. Si existe una corriente circulando desde un punto A a uno B y el potencial eléctrico aumenta (VB > VA) es porque se está introduciendo energía en el sistema eléctrico. Si por el contrario el potencial disminuye (VA > VB) la energía se está sacando del sistema eléctrico. Esto es cierto tanto para resistencias como para motores o generadores.
8.1 Efecto Joule
En el caso particular de una resistencia el potencial final es siempre menor que el inicial, de manera que tenemos

esta es la llamada ley de Joule (o efecto Joule). En una resistencia eléctrica se disipa energía eléctrica. Esta energía o bien se radia al exterior en forma de calor (que es la base de las estufas y calefactores de resistencia) o bien queda como un aumento de la energía interna (lo que se ve como un aumento de la temperatura del cable), o ambas cosas a la vez.
Alternativamente esta potencia puede escribirse

9 Generadores
Es fácil demostrar que en un circuito cerrado no es posible que se cumple la ley de Ohm en todos sus puntos. Supongamos dos puntos del circuito P y N tales que VP > VN y que estos puntos están conectados por un cable de resistencia R en este caso habrá una corriente fluyendo de P a N y en el cable la densidad de corirnte y el campo eléctrico irán en el mismo sentido. Pero, ¿qué ocurre al cerrar el circuito? Para obtener una corriente continua la intensidad de corriente debe ir de N a P por el resto del circuito, pero el campo eléctrico, que va de mayor a menor potencial, va de P a N. Por tanto, debe haber una porción de circuito en la cual la densidad de corriente vaya en sentido contrario al campo eléctrico. La parte del circuito en que esto ocurre se denomina el generador (o fuente).
Un circuito en el que la corriente viajara siempre “cuesta abajo” es tan imposible como la cascada del grabado de Escher (en realidad, algo menos imposible).

Un generador es entonces un elemento de circuito en el que la densidad de corriente va en sentido opuesto al campo eléctrico (no cumpliéndose por tanto la ley de Ohm) o en términos de circuitos, que la corriente va de menor a mayor potencial. Un generador, por tanto, viene a ser equivalente a una bomba que eleva el agua hasta una cierta altura, venciendo la fuerza de la gravedad.
Para hacerlo debe haber una fuerza actuando sobre las cargas, además de la fuerza eléctrica
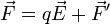
Esta fuerza adicional no puede ser debida a un campo electrostático. Entre los distintos tipos de generadores tenemos fuerzas:
- Mecánicas, en la que la carga es arrastrada contra el campo eléctrico.
- Químicas, como en las pilas o baterías, donde una reacción química separa las cargas positivas de las negativas.
- Magnéticas, como en los generadores industriales, alternadores o dinamos.
- Eléctricas no electrostáticas. En el fenómeno de la inducción electromagnética, un campo magnético variable es capaz de producir un campo eléctrico lo que también se aplica en alternadores y dinamos.
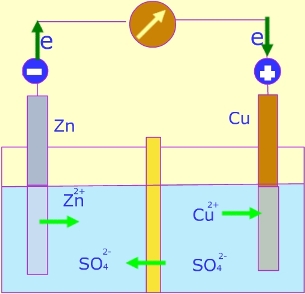
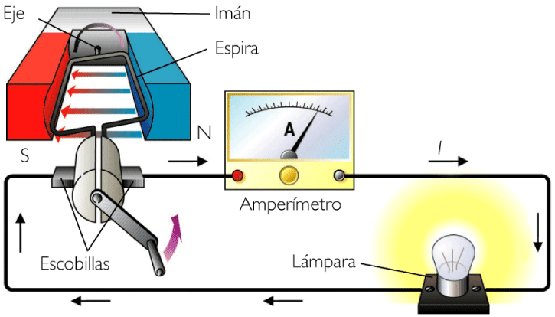

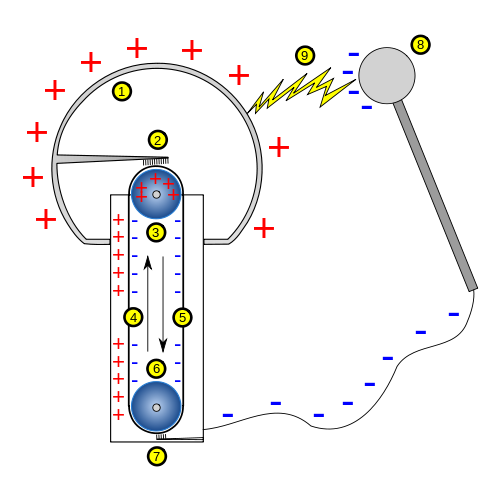
El modelo más sencillo de generador mecánico es el Van de Graaff, encontrándose el más grande del mundo en el Museo de la Ciencia de Boston. Un generador van de Graaff se basa en primer lugar en separación de carga por fricción (o de otras formas) y su arrastre por una cinta aislante. Mediante un par de electrodos se consigue acumular carga positiva en un sitio (la corona exterior en el esquema) y negativa en otro (la tierra y el electrodo a tierra). En el propio generador el campo va de las cargas positivas a las negativas (hacia abajo en el esquema) pero la corriente va en sentido contrario (en el esquema descienden cargas negativas, lo que supone una corriente hacia arriba).
El circuito se cierra colocando algún cable o simplemente por descargas a través del aire. En el exterior la corriente va de las cargas positivas a las negativas, como es de esperar.
Todos los generadores se caracterizan por tener un polo positivo o ánodo (P) y un polo negativo o cátodo (N), en los que se acumulan las cargas de cada signo. La separación de cargas produce un campo eléctrico que tiende a reunirlas. La separación es conseguida por las fuerzas no electrostáticas que igualan o superan a las eléctricas.
La fuerza por unidad de carga puede escribirse en la forma
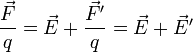
donde 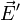 no es un verdadero campo eléctrico, sino un campo efectivo, que mide la fuerza adicional que actúa sobre las cargas. Este campo efectivo solo existe dentro de los generadores.
no es un verdadero campo eléctrico, sino un campo efectivo, que mide la fuerza adicional que actúa sobre las cargas. Este campo efectivo solo existe dentro de los generadores.
9.1 Fuerza electromotriz y resistencia interna
Para medir cómo de potente es un generador se define la fuerza electromotriz (f.e.m.) 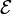 . Para ello se considera una curva cerrada que va del polo positivo al negativo del generador por su exterior y de N a P por el interior. La fuerza electromotriz es igual al trabajo por unidad de carga para recorrer esta curva cerrada
. Para ello se considera una curva cerrada que va del polo positivo al negativo del generador por su exterior y de N a P por el interior. La fuerza electromotriz es igual al trabajo por unidad de carga para recorrer esta curva cerrada
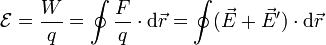
De la definición se ve que la f.e.m. no es una fuerza en absoluto, ya que se mide en voltios (V).
9.1.1 Valor en circuito abierto
Un circuito está abierto cuando hay una interrupción en él que impide que circule la corriente (por ejemplo, una pila no conectada a nada estaría en circuito abierto). La fuerza electromotriz se puede descomponer en suma de dos integrales
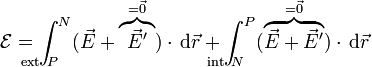
En el tramo exterior el campo efectivo es nulo porque éste solo existe dentro de los generadores. En el interior, puesto que no hay corriente y las cargas están en reposo, la fuerza sobre cada una se anula
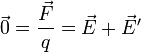
por lo que la fuerza electromotriz se reduce a
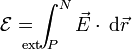
pero esta integral no es otra que la diferencia de potencial
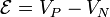
Por tanto, la diferencia de potencial entre los polos coincide con la fuerza electromotriz en circuito abierto. Esto nos proporciona un método sencillo de medir la f.e.m de una fuente: basta colocar un voltímetro entre sus polos cuando no está conectada a nada.
9.1.2 Valor en circuito cerrado
Cuando la fuente está conectada a un circuito ya habrá en general una corriente circulando por su interior. Al salir la corriente del polo positivo y llegar al negativo se está produciendo una descarga parcial de los polos. Aunque el campo efectivo sigue separando las cargas por dentro del generador, parte de ellas vuelven por fuera. Al reducirse la cantidad de carga en los polos, el campo eléctrico se reduce y ya dentro del generador
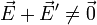
la reducción del campo eléctrico depende de cuanta carga se está escapando de los polos en cada momento, es decir de cuánta corriente está circulando. En primera aproximación, será proporcional a la corriente y podemos escribir
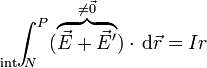
siendo r una constante de proporcionalidad que depende de la naturaleza del generador. A esta constante se la denomina resistencia interna. Con este cambio, la f.e.m. equivale a
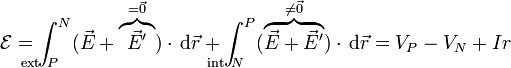
y despejando
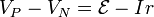
En un circuito cerrado la diferencia de potencial entre los polos es menor que la f.e.m. de la fuente. La diferencia la da el término Ir que podemos leer como la d.d.p. en una resistencia r.
El circuito equivalente a una fuente de tensión real está formado por dos elementos: una fuente ideal (sin resistencia interna) puesta en serie con una resistencia r.
9.2 Ley de Ohm generalizada
Supongamos que tenemos un circuito sencillo formado por un generador real al que se conecta una resistencia R (como podría ser una bombilla). En este caso, tenemos por un lado que
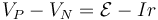
y por otro dado, que es esta d.d.p. la que alimenta la bombilla
Igualando y despejando nos queda
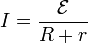
que constituye la ley de Ohm generalizada: la corriente en un circuito simple es igual a la f.e.m. dividida por la suma de todas las resistencias, tanto externas como internas.
En este caso la tensión a la salida de la fuente es
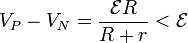
9.3 Ley de Kirchhoff para las mallas
La ecuación anterior se generaliza un circuito general. Una malla es un circuito cerrado, auqnue puede tener derivaciones, de forma que la intensidad de corriente no tiene el mismo valor en todos los puntos. Además puede haber varios generadores en la malla. En ese caso, cuando recorremos la malla se verifica
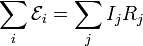
donde las Rj son todas las resistencias (tanto internas como externas) e Ij es la corriente que va por cada una. Las fuerzas electromotrices son posiitivas si se recorren del polo negativo al positivo, y negativas si se recorren en sentido contrario.
Esta es la ley de Kirchhoff para las mallas (o segunda ley de Kirchhoff).
En muchos casos, en lugar de trabajar directamente con esta ley es preferible emplear los voltajes de los distintos nodos y razonar a partir de ellos.
9.4 Potencia de un generador
Un generador tiene también un aspecto energético. Sabemos que en una resistencia se disipa energía por efecto Joule. Por la ley de conservación de la energía, el calor producido debe entrar en otra parte en forma de calor o trabajo. Esta otra parte es el generador. Recordemos que dentro de un generador la corriente va del polo negativo al positivo, por lo que tenemos,
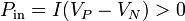
es decir, en el interior del generador se está produciendo energía eléctrica.
¿De donde procede esta energía? De la fuerza no eléctrica que está actuando sobre las cargas. Como la bomba de agua, este fuerza está subiendo las cargas de potencial, realizando un cierto trabajo. Puede ser trabajo mecánico, o puede provenir de la liberación de energía almacenada en los enlaces químicos. En un sistema aislado, esta energía termina agotándose y la corriente se detiene. Esto es lo que ocurre al descargarse una pila. En la batería de un automóvil se produce una recarga continua a partir de la energía procedente de la combustión de la gasolina. Si no hay recarga (como ocurre al dejarse las luces encendidas por la noche) la batería se termina agotando.
La potencia neta que entra en el generador y es transmitida al resto del circuito se puede escribir
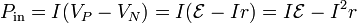
que podemos leer como que un generador ideal produce una potencia 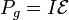 , pero no toda esa potencia se entrega al circuito, porque parte se consume en él mismo, debido a la resistencia interna (por eso las pilas se calientan).
, pero no toda esa potencia se entrega al circuito, porque parte se consume en él mismo, debido a la resistencia interna (por eso las pilas se calientan).
En el ejemplo del generador real con la bombilla tenemos que, por el lado del generador
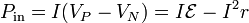
y por el lado de la bombilla
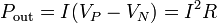
siendo iguales ambas cantidades

que leemos que de la energía procedente del generador ideal parte se va en la resistencia interna y parte en la externa.






