Aprovechamiento máximo del calor
De Laplace
Contenido |
1 Enunciado
Se desea caldear una habitación a 22°C cuando la temperatura de la calle es de 5°C. Para ello se dispone de un ladrillo de 50 kg de hierro que previamente se ha calentado a 200°C.
Si se coloca el ladrillo directamente en la habitación, ¿cuánto calor se libera? ¿Cuánta entropía se produce?
Supongamos que en lugar de meter el ladrillo se usa como foco caliente de una máquina reversible que alimenta una bomba de calor también reversible. En ese caso, ¿cuánto calor entra en la habitación? ¿Cuánta entropía se produce?
Dato: Calor específico del hierro 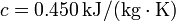
2 Calor liberado directamente
Si calentamos la habitación simplemente depositando el bloque en la habitación, la cantidad de calor que libera es la correspondiente al descenso de temperatura desde su valor inicial, que llamaremos T1 a T0, la temperatura de la habitación (que, por ser de gran tamaño supondremos un baño térmico). Este calor es
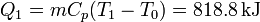
3 Variación de entropía
Existen dos cambios en la entropía, uno en el bloque de hierro, que al enfriarse ve reducida su entropía, y otro en la habitación que al recibir calor la ve incrementada.
3.1 Variación en el ambiente
La habitación recibe calor a una temperatura constante T0, por lo que su aumento de entropía es simplemente
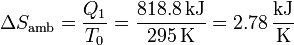
3.2 Variación en el bloque
La variación para el bloque la calculamos suponiendo un proceso reversible, consistente en que su temperatura va bajando gradualmente, siendo uniforme en el bloque en todo momento. En ese caso
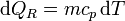

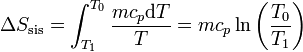
siendo su valor numérico
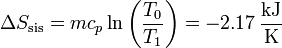
3.3 Variación total
Sumando los dos incrementos
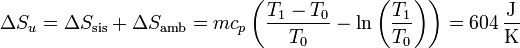
La variación neta es positiva, como corresponde a un proceso posible e irreversible.
4 Trabajo perdido
Parecería que colocar el bloque en la habitación es la forma más eficiente de calentar ésta, ya que todo el calor saliente va a parar a ella. Sin embargo, no lo es. Desde el mismo momento que hay producción de entropía y el proceso es irreversible, es claro que debe haber algún proceso más eficiente que sea reversible.
La causa de la irreversibilidad es la diferencia finita de temperaturas. El calor se derrama por la habitación como el agua que cae por una cascada. Pero al igual que en la cascada se puede colocar una central hidroeléctrica, entre la salida de calor del bloque y su llegada a la habitación se podría poner una máquina térmica reversible que aprovechara parte del calor para producir trabajo útil.
En un momento dado el bloque se encontrará a una temperatura T y cederá reversiblemente un calor − mcpdT (el signo porque la temperatura disminuye, dT es negativo, pero el calor cedido es positivo respecto de la máquina). Con ese calor la máquina hará un trabajo también diferencial
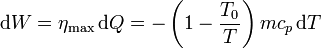
Integrando obtenemos el trabajo perdido, que podríamos haber aprovechado con esta máquina térmica
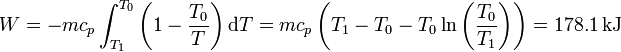
esto es, podríamos haber aprovechado el 21% del calor cedido.
5 Relación con la entropía
Es inmediato comprobar que el trabajo perdido es igual al incremento de entropía multiplicado por la temperatura ambiente
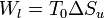
Por tanto, vemos que existe una asociación directa entre la producción de entropía y el trabajo aprovechable que podríamos haber sacado del sistema.
Esta ecuación es un caso particular de la relación
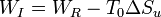
que nos dice que el trabajo producido en un proceso irreversible (en nuestro caso, ninguno) es igual al calor que podríamos producir reversiblemente (el máximo, en nuestro caso el que hemos calculado) menos que lo que se pierde producción de entropía (en nuestro caso, todo).
Cuando la temperatura del foco frío, en nuestro caso la habitación, es la del ambiente y el bloque se considera finalmente en el estado muerto, ese trabajo máximo que podría extraerse es la llamada exergía del sistema.
6 Calor extra aprovechable
Si extraemos el trabajo aprovechable, la cantidad de calor que el ladrillo mete directamente en la habitación se ve reducido. Pasa a ser
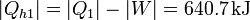
Parece entonces que estamos peor que antes, pues el bloque estaría calentando menos la habitación. No es así, porque ahora tenemos 178 kJ de trabajo a nuestra disposición para aprovechar como queramos.
Y la forma más eficiente es usarlo para hacer funcionar una bomba de calor entre el exterior (a 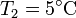 ) y la habitación. La cantidad máxima de calor que introducimos la da el coeficiente de desempeño de una bomba de calor reversible
) y la habitación. La cantidad máxima de calor que introducimos la da el coeficiente de desempeño de una bomba de calor reversible
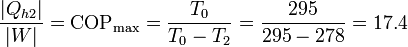
Esto quiere decir que podemos bombear al interior una cantidad de calor
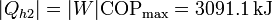
El calor total que introducimos es la suma del de desecho del bloque metálico más el que mete la bomba
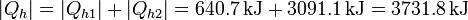
Esta cantidad es considerablemente superior a la que sacaríamos directamente del bloque
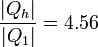
Este valor que hemos indicado es el máximo posible suponiendo el bloque finalmente a temperatura de la habitación, ya que todos los procesos implicados son reversibles. Para este proceso doble (bloque que alimenta una máquina térmica reversible, que mueve una bomba de calor también reversible) la producción de entropía es 0 y no hay trabajo perdido.
7 Un refinamiento adicional
Todavía podemos mejorar un poco este resultado. El bloque está finalmente a 22°C, pero el exterior está a 5°C. Si no le tenemos especial aprecio al bloque podemos sacarlo al exterior y aprovechar la pequeña diferencia de temperaturas para sacar un poco más de trabajo y bombear algo más de calor al interior.
El trabajo extra que podríamos obtener sería
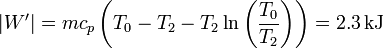
que nos proporciona un calor extra
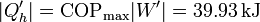
lo que eleva nuestro calor total a
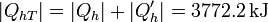
elevando nuestra eficiencia a 4.60 veces el calor original.
En términos de la exergía, este refinamiento consiste en variar la naturaleza del estado muerto. Antes considerábamos que era a 22°C, la temperatura de la habitación. A partir de ahí el bloque no podía dar nada más. Sin embargo, la exaergía depende tanto del sistema como del ambiente. Si consideramos que el ambiente es el exterior, a 5°C, un bloque a 22°C aun tiene algo de exergía aprovechable, que es lo que acabamos de hallar.
8 Un método alternativo
Una vez que hemos visto un método concreto para incrementar el calor introducido en la habitación, pueden pensarse alternativas similares. Una de ellas es la siguiente: Puesto que el rendimiento de una máquina térmica es mayor cuanto menor sea la temperatura del foco frío, ¿por qué no hacerla funcionar entre la temperatura inicial (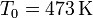 ) y la temperatura exterior (
) y la temperatura exterior (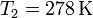 )?
)?
En este caso, el trabajo que sacaríamos del bloque sería
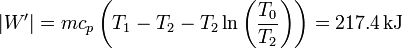
esto es, un 22% más de trabajo aprovechable.
Con este trabajo hacemos funcionar la máquina de calor entre el exterior y la habitación, introduciendo una cantidad máxima de calor
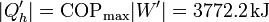
En este caso este sería el único calor que habría que contar, ya que al usar el exterior como foco frío de la máquina térmica, no estaríamos arrojando el calor de derecho del bloque en su interior (o, para ser precisos, esta incluido en el calor bombeado).
Vemos que, por este un proceso reversible, la cantidad máxima de calor que obtenemos es exactamente la misma que en el proceso anterior, también reversible, incluyendo el refinamiento. Esto es consecuencia de que la exergía es una función de estado. Dado un estado inicial y un estado muerto final, la cantidad máxima de trabajo que podemos extraer es la misma, independientemente del proceso.





