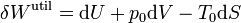Introducción a la exergía
De Laplace
Contenido |
1 Concepto
La exergía es una medida de la disponibilidad de la energía. La idea es que parte de la energía de un sistema se puede aprovechar para realizar trabajo mecánico, eléctrico o de otro tipo. El segundo principio de la termodinámica nos establece limitaciones en cuanto a la cantidad de trabajo que podemos realizar. Pero existe además una limitación práctica en cuanto a que sólo se puede realizar trabajo si el sistema almacena una energía respecto al ambiente que le rodea.
Por ejemplo, consideremos el agua situada en un embalse a cierta altura. Este agua puede emplearse para mover turbinas y generar energía eléctrica, pero, una vez que todo el agua ha bajado al nivel del mar, ya no se puede seguir aprovechando. Hay un límite en la energía disponible asociado a la diferencia de altura entre el agua del embalse y el entorno. Cuando este desnivel desaparece, ya no hay más energía disponible.
Supongamos un recipiente que contiene un gas a alta presión y alta temperatura. Si hacemos un orificio en el recipiente y dejamos que salga el aire a la atmósfera, perdemos toda la energía disponible, ya que rápidamente su presión se iguala a la atmosférica y en poco tiempo su temperatura se iguala la del aire que lo rodea. Hemos desperdiciado toda la energía disponible o exergía.
En cambio, podíamos haber usado el que la presión era superior a la atmosférica para producir un trabajo mecánico, moviendo un pistón, y podíamos haber usado el que su temperatura era superior a la atmosférica para alimentar una máquina térmica, es decir, que tanto la diferencia de presiones como la diferencia de temperaturas eran aprovechables para realizar trabajo útil.
Se denomina “exergía” a la cantidad máxima de energía que puede transformarse en trabajo útil, entendiendo por útil el que no se emplea en actuar contra el ambiente.
La exergía se consume por completo cuando la presión y la temperatura (y el resto de variables de estado como la altura sobre el nivel del mar, el voltaje, etc. que lo diferencian de lo que le rodea) se igualan a la del entorno. Una vez que se iguala la temperatura del sistema con la del ambiente (alcanzándose el equilibrio térmico) y se iguala su presión con la exterior (llegándose al equilibrio mecánico), ya no se puede extraer energía adicional. Se dice que en ese caso el sistema ha alcanzado el “estado muerto”.
2 Caso de un sistema cerrado fluido
El cálculo de la exergía es muy general y puede aplicarse a todo tipo de sistemas físicos. En esta introducción nos limitaremos a considerar el caso sencillo de un sistema fluido (un gas) que se encuentra a una cierta presión p y temperatura T diferentes de la presión p0 y temperatura T0 del aire que lo rodea.
Calcularemos por separado la cantidad máxima de trabajo que podemos obtener por la diferencia de presiones y por la diferencia de temperaturas. La suma de las dos cantidades nos permitirá hallar la exergía del sistema.
2.1 Aprovechamiento del trabajo
Puesto que estamos interesados en el máximo aprovechamiento de la energía, debemos considerar procesos en los que no se produzca entropía en el universo, es decir, deben ser cuasiestáticos y reversibles. En este caso, el trabajo realizado sobre el sistema vale
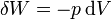
Estamos interesados en los procesos en el que este trabajo resulta negativo, ya que en ese caso es el gas el que realiza trabajo sobre el entorno.
Ahora bien, este trabajo no es todo trabajo útil. Una parte de él se emplea en desplazar el aire exterior, que está a presión p0. Este desplazamiento del ambiente se diluye en la masa y no es aprovechable. Por ello, hacemos la descomposición siguiente
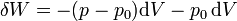
De estos dos términos, sólo el primero es trabajo útil. El segundo representa el trabajo para desplazar el aire de alrededor. Por ejemplo, en un sistema de un gas con un muelle el primer término sería el trabajo para comprimir el muelle (que queda almacenado como energía elástica y puede ser usado más adelante) mientras que el segundo es el trabajo de expansión contra la presión externa, que se pierde.
En un proceso cíclico la integral del segundo término se anula (ya que p0 es constante y ΔV = 0 en un ciclo) lo que quiere decir que si al final estamos como al principio ese trabajo de desplazamiento del aire exterior es recuperado cuando vuelve a ocupar su lugar.
Nos queda entonces la relación
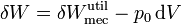
2.2 Aprovechamiento del calor
Por estar a una temperatura diferente a la del ambiente, podemos aprovechar esta diferencia par alimentar una máquina térmica que funcione entre la temperatura del sistema y la del ambiente.
El trabajo máximo lo obtendremos con una máquina reversible que opere entre las dos temperaturas. Dado que la temperatura del sistema va cambiando (a medida que se va acercando al equilibrio térmico), esta hipotética máquina es muy especial, ya que funciona con una entrada a temperatura variable. Puesto que se trata de establecer un máximo, podemos admitir esta hipótesis, sabiendo una máquina real no podría hacer tal cosa (habría que sustituirla por una serie de máquinas que actuarían consecutivamente).
En un momento dado, el sistema posee una temperatura absoluta T y cede a la máquina una cantidad de calor | δQ | . El trabajo proporcionado por esta máquina sería, por el teorema de Carnot
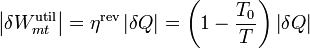
El valor absoluto se debe a que el calor que entra en la máquina sale del sistema. Si consideramos positivo el calor que entra en el sistema, este δQ es negativo. Lo mismo ocurre con el trabajo. Esta fórmula nos da el trabajo realizado por la máquina sobre el exterior. si consideramos positivo el trabajo que va hacia adentro, éste es negativo.
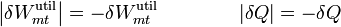
Al sustituir esto se van los dos signos y queda simplemente
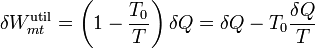
Pero, por tratarse de un proceso reversible, se cumple
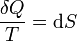
Por tanto, obtenemos para el trabajo producido por la diferencia de temperaturas

2.3 Exergía
Sumando las dos contribuciones obtenemos el trabajo total útil
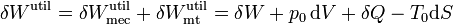
pero, por el primer principio de la termodinámica
por lo que queda