Esfera conductora hueca con carga puntual GIA

De Laplace

Revisión a fecha de 11:36 18 mar 2012; Gabriel (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución
- 2.1 Carga eléctrica en las superficies del conductor
- 2.2 Potencial electrostático del sistema

1 Enunciado

Una esfera conductora hueca de radios interior

R 1

y exterior

R 2

tiene en su centro una pequeña partícula cargada con carga

q

. Suponiendo que la esfera no tiene carga neta y que está aislada calcule el potencial al que se encuentra y la carga que hay en sus superficies interior y exterior.

2 Solución

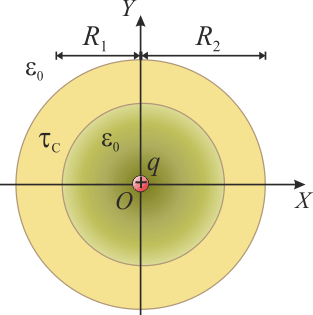
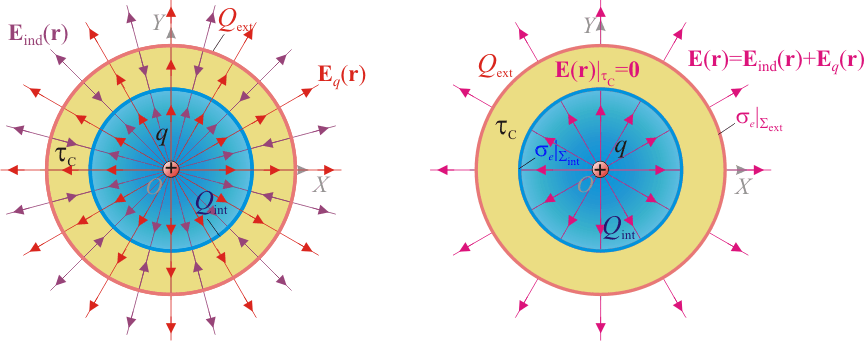
En la figura se muestra una sección transversal del sistema bajo estudio. Se trata de una esfera conductora de radio $R 2$ , descargada y aislada, en cuyo interior hay un hueco esférico y concéntrico de radio $R 1$ , que se encuentra vacío salvo en su centro $O$ , donde hay situada una carga puntual de valor $q$ . Ésta carga produce una campo eléctrico radial con centro en la carga (es decir, en el punto $O$ ),

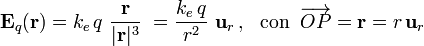
$\mathbf{E}_q(\mathbf{r})=k_e\!\ q \ \frac{\mathbf{r}}{|\mathbf{r}|^3}\ =\frac{k_e\!\ q}{r^2}\ \mathbf{u}_r\,\mathrm{,}\;\;\;\mathrm{con}\;\;\overrightarrow{OP}=\mathbf{r}=r\!\ \mathbf{u}_r$

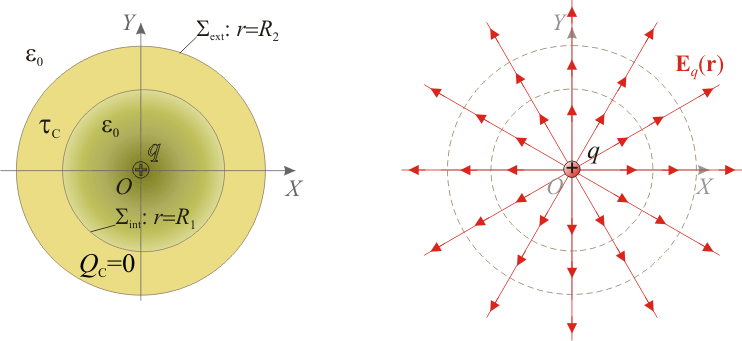
definido en todos los puntos del espacio. Si la carga puntual, que supondremos positiva, se encuentra en el hueco de la esfera conductora, este campo eléctrico arrastrará las cargas libres negativas del conductor hacia la superficie interior 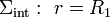$\Sigma_\mathrm{int}:\ r=R_1$ , a la vez que desplazaría las posibles cargas libres positivas hacia la exterior, 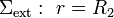$\Sigma_\mathrm{ext}:\ r=R_2$ , induciéndose en dichas superficies sendas densidades superficiales de carga de signo opuesto. Y como el conductor está descargado y aislado su carga eléctrica total $Q C$ debe ser siempre nula. Por tanto, las cantidades de carga inducidas en las superficies $Σ int$ y $Σ ext$ debe ser opuestas:

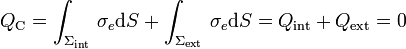
$Q_\mathrm{C}=\int_{\Sigma_\mathrm{int}}\!\ \sigma_e\mathrm{d}S+\int_{\Sigma_\mathrm{ext}}\!\ \sigma_e\mathrm{d}S=Q_\mathrm{int}+Q_\mathrm{ext}=0$

Pero, aunque la cantidad total de carga inducida es nula, al estar separada espacialmente en sendas distribuciones de signo opuesto, éstas crearán un campo eléctrico (que llamaremos “inducido”) 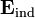$\mathbf{E}_\mathrm{ind}$ . El sistema alcanza el equilibrio cuando este campo anula al campo de la carga puntual en el interior de la región conductora $τ C$ comprendida entre las superficies esféricas $Σ int$ y $Σ ext$ . Es decir,

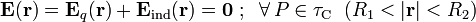
$\mathbf{E}(\mathbf{r})=\mathbf{E}_q(\mathbf{r})+\mathbf{E}_\mathrm{ind}(\mathbf{r})=\mathbf{0}\,\,\mathrm{;}\,\;\;\forall\, P\in \tau_\mathrm{C}\;\;(R_1<|\mathbf{r}|<R_2)$

2.1 Carga eléctrica en las superficies del conductor

Para determinar la carga eléctrica en la superficie interior de la corteza conductora aplicamos la ley de Gauss utilizando una superficie gaussiana cerrada 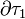$\partial\tau_1$ tal que todos sus puntos estén dentro de la región conductora $τ C$ . Por ejemplo, podemos tomar como 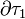$\partial \tau_1$ una superficie esférica con centro en $O$ y radio $r$ , tal que $R 1 < r < R 2$ . En cada punto de esta superficie el campo eléctrico total es nulo por ser punto del interior del conductor en equilibrio. Por tanto, el flujo de dicho campo y, en consecuencia, la cantidad total de carga eléctrica encerrada por 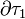$\partial\tau_1$ , es...

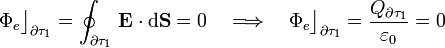
$\Phi_e\big\rfloor_{\partial\tau_1}=\oint_{\partial\tau_1}\!\ \mathbf{E}\cdot\mathrm{d}\mathbf{S}=0\quad\Longrightarrow\quad\Phi_e\big\rfloor_{\partial\tau_1}=\frac{Q_{\partial\tau_1}}{\varepsilon_0}=0$

La carga eléctrica en el interior de 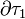$\partial\tau_1$ es la carga puntual $q$ , más la carga distribuida en la superficie interior $Σ int$ de la corteza conductora. Obsérvese que no hay carga eléctrica neta en el volumen de dicha corteza comprendido entre las superficies $Σ int$ y 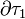$\partial\tau_1$ , ya que se trata de una región conductora en equilibrio. De esta forma,

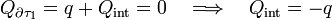
$Q_{\partial\tau_1}=q+Q_\mathrm{int}=0\quad\Longrightarrow\quad Q_\mathrm{int}=-q$

Y aplicando ahora que el conductor está descargado y aislado y que, por tanto, las cantidades de carga en sus superficies deben ser opuestas...

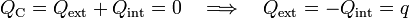
$Q_\mathrm{C}=Q_\mathrm{ext}+Q_\mathrm{int}=0\quad\Longrightarrow\quad Q_\mathrm{ext}=-Q_\mathrm{int}=q$

2.2 Potencial electrostático del sistema

Una vez calculada la cantidad de carga que hay en la superficie externa del conductor, pasamos a discutir cómo se distribuye. En primer lugar, hay que tener en cuenta que en el interior de la región conductora no hay campo eléctrico. Esto tiene como consecuencia que la densidad de carga eléctrica en la superficie $Σ ext$ sólo está relacionada con el campo eléctrico en el exterior:

$\mathbf{n}\cdot\bigg[\mathbf{E}(r=R_2^+)-\underbrace{\mathbf{E}(r=R_2^-)}_{=\mathbf{0}}\bigg]_{\Sigma_\mathrm{ext}}=\mathbf{n}\cdot\mathbf{E}(r=R_2^+)=\frac{\sigma_e}{\varepsilon_0}\bigg\rfloor_{\Sigma_\mathrm{ext}}$

(consecuencia de la discontinuidad del campo en la superficie cargada). Es decir, la región conductora actúa como una pantalla de manera que la carga puntual $q$ y la densidad superficial de carga en la superficie interior no afectan en absoluto a la forma de distribuirse la carga en $Σ ext$ . Y como no hay otras cargas en el exterior de dicha superficie esférica y si, además, asumimos que es homogénea, la carga eléctrica $Q ext = q$ se distribuirá uniformemente, con una densidad superficial,

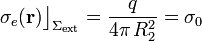
$\sigma_e(\mathbf{r})\big\rfloor_{\Sigma_\mathrm{ext}}=\frac{q}{4\pi\!\ R_2^2}=\sigma_0$

Obsérvese que de la discusión anterior acerca del “efecto pantalla” del conductor se deduce que el campo eléctrico resultante en el exterior de la esfera conductora depende exclusivamente de aquella distribución uniforme y esférica. Y, como sabemos, una distribución de carga de este tipo produce un campo eléctrico radial idéntico al que crearía una carga puntual $q$ en el centro de la distribución (consecuencia de la aplicación de la ley de Gauss).

Esfera conductora hueca con carga puntual GIA

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Carga eléctrica en las superficies del conductor

2.2 Potencial electrostático del sistema

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES