Partícula que se despega de esfera
De Laplace
Contenido |
1 Enunciado
Una partícula de masa m se encuentra inicialmente en reposo en el punto superior de una esfera de radio R apoyada en el suelo. La partícula desliza sin rozamiento sobre la superficie de la esfera.
- Determine el punto de la esfera en el que la partícula se despega de ella.
- ¿Qué rapidez tiene la partícula en el momento en que impacta con el suelo?
- Calcule el punto en el el que la masa impacta en el suelo.
2 Punto de separación
Lo que determina que la partícula se separe de la esfera es que ésta no sea capaz de retenerla, esto es, se trata de un vínculo unilateral.
Si tuviéramos, en vez de una partícula sobre una esfera, una anilla ensartada en un aro, la anilla nunca se separaría de la trayectoria circular, ya que el aro se lo impediría. El mecanismo consiste en que el aro ejerce una fuerza de reacción que puede ir tanto hacia adentro como hacia afuera. Para la partícula apoyada en la esfera, en cambio, la fuerza de reacción solo puede ir hacia afuera, no hacia adentro, no siendo capaz de retener a la partícula sobre su superficie.
En todo momento en que la partícula está sobre la esfera, la ecuación de movimiento es
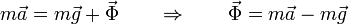
Inicialmente, cuando la partícula está en reposo en lo alto de la esfera, la reacción compensa exactamente al peso y va dirigida hacia afuera





