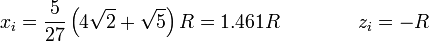Partícula que se despega de esfera

De Laplace

Contenido

1 Enunciado
2 Punto de separación
3 Rapidez de impacto
4 Punto de impacto

1 Enunciado

Una partícula de masa $m$ se encuentra inicialmente en reposo en el punto superior de una esfera de radio $R$ apoyada en el suelo. La partícula desliza sin rozamiento sobre la superficie de la esfera.

Determine el punto de la esfera en el que la partícula se despega de ella.
¿Qué rapidez tiene la partícula en el momento en que impacta con el suelo?
Calcule el punto en el el que la masa impacta en el suelo.

2 Punto de separación

Lo que determina que la partícula se separe de la esfera es que ésta no sea capaz de retenerla, esto es, se trata de un vínculo unilateral.

Si tuviéramos, en vez de una partícula sobre una esfera, una anilla ensartada en un aro, la anilla nunca se separaría de la trayectoria circular, ya que el aro se lo impediría. El mecanismo consiste en que el aro ejerce una fuerza de reacción que puede ir tanto hacia adentro como hacia afuera. Para la partícula apoyada en la esfera, en cambio, la fuerza de reacción solo puede ir hacia afuera, no hacia adentro, no siendo capaz de retener a la partícula sobre su superficie.

En todo momento en que la partícula está sobre la esfera, la ecuación de movimiento es

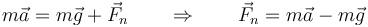
$m\vec{a}=m\vec{g}+\vec{F}_n\qquad\Rightarrow\qquad \vec{F}_n=m\vec{a}-m\vec{g}$

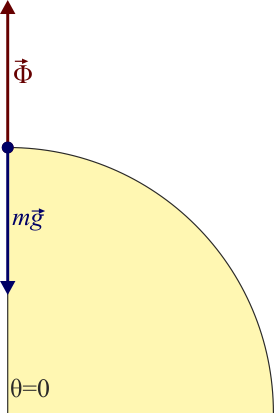
Inicialmente, cuando la partícula está en reposo en lo alto de la esfera, la reacción compensa exactamente al peso y va dirigida hacia afuera.

A medida que la partícula se va cayendo, se mueve con mayor rapidez, lo que implica una aceleración normal (radial y hacia adentro) cada vez más elevada. Por otro lado, la componente normal del peso es cada vez más pequeña (ya que depende de la latitud sobre la esfera, siendo máxima en el polo norte y nula en el ecuador). Mientras la componente normal de la gravedad supere a la aceleración normal, la reacción de la esfera irá hacia el exterior. Sin embargo, se llega a un punto en el que la aceleración normal iguala a la componente normal de la gravedad. Para que a partir de ahí la partícula siguiera sobre la esfera, debería ser la reacción la que produjera la aceleración normal, apuntando hacia adentro, lo cual es imposible.

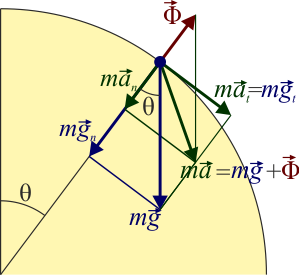
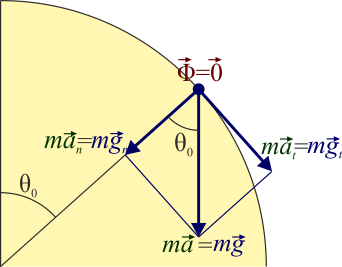
La separación se produce, por tanto, en el momento en el que la fuerza de reacción vincular se anula, lo cual coincide con el momento en el que la aceleración normal coincide con la componente normal de la gravedad.

Llamando $θ$ al ángulo que forma con la vertical el vector de posición relativo al centro, tenemos la componente tangencial de la ecuación de movimiento

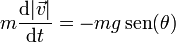
$m\frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}=-mg\,\mathrm{sen}(\theta)$

y la componente normal

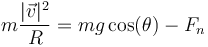
$m\frac{|\vec{v}|^2}{R}=mg\cos(\theta)-F_n$

El signo negativo se debe a que la dirección normal a la trayectoria va hacia adentro y la fuerza de reacción va hacia afuera.

La condición de separación será entonces

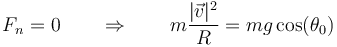
$F_n = 0 \qquad \Rightarrow\qquad m\frac{|\vec{v}|^2}{R}=mg\cos(\theta_0)$

Esta ecuación relaciona el ángulo en el que se produce la separación con la rapidez en se momento. Para poder determinar ambas cantidades necesitamos una ecuación adicional.

La más sencilla es la ley de conservación de la energía mecánica. La fuerza de reacción es normal en todo momento a la trayectoria, por lo que no realiza trabajo alguno. Por tanto, la única energía potencial que debemos considerar es la correspondiente al peso. Se cumple entonces

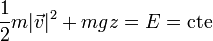
$\frac{1}{2}m|\vec{v}|^2+mgz = E = \mathrm{cte}$

Como origen de energía potencial podemos tomar el centro de la esfera (también es razonable, e igual de simple, tomar el punto inicial como referencia, o el polo sur de la esfera, en el que ésta se apoya en el suelo; todas las elecciones conducen al mismo resultado). En este caso, la energía cinética inicial es nula, mientras que la energía potencial vale $m g R$ . La ley de conservación de la energía mecánica nos da entonces

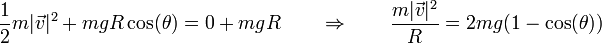
$\frac{1}{2}m|\vec{v}|^2 +mgR\cos(\theta) = 0 + m g R\qquad\Rightarrow\qquad \frac{m|\vec{v}|^2}{R} = 2mg(1-\cos(\theta))$

Llevando esto a la condición de separación

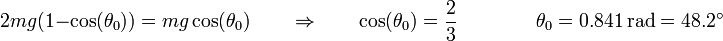
$2mg(1-\cos(\theta_0)) = mg\cos(\theta_0)\qquad\Rightarrow\qquad \cos(\theta_0) = \frac{2}{3}\qquad\qquad \theta_0 = 0.841\,\mathrm{rad}=48.2^\circ$

El punto de separación se encuentra a una altura $2 R / 3$ desde el ecuador de la esfera o $5 R / 3$ desde el punto de apoyo.

3 Rapidez de impacto

Una vez que la partícula se separa de la esfera describe un movimiento parabólico, siendo su aceleración la de la gravedad.

Para hallar la rapidez de la partícula en el momento en que impacta con el suelo, podríamos emplear las ecuaciones horarias del tiro parabólico. Sin embargo, no es necesario, ya que se sigue cumpliendo la ley de conservación de la energía mecánica y por tanto, sigue siendo cierto que

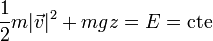
$\frac{1}{2}m|\vec{v}|^2+mgz = E = \mathrm{cte}$

siendo además $E$ el mismo valor de la energía que calculamos anteriormente, $E = m g R$ .

En el momento del impacto $z = - R$ (ya que estamos midiendo la altura desde el centro de la esfera. Esto nos da la rapidez

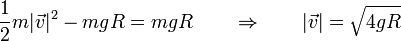
$\frac{1}{2}m|\vec{v}|^2 - mgR = mg R \qquad\Rightarrow\qquad |\vec{v}| = \sqrt{4gR}$

que es el mismo valor de la rapidez que tendría si cayera verticalmente desde el punto inicial.

4 Punto de impacto

Para determinar el punto de impacto sí necesitamos las ecuaciones horarias o, al menos, la ecuación de la trayectoria.

Una vez que se separa de la esfera, la partícula describe un movimiento parabólico con aceleración la de la gravedad

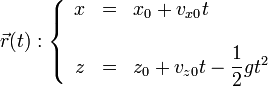
$\vec{r}(t):\left\{\begin{array}{rcl} x & = & x_0 + v_{x0}t \\ && \\ z & = & \displaystyle z_0+v_{z0}t-\frac{1}{2}gt^2\end{array}\right.$

Aquí la posición y la velocidad iniciales son las que tiene la partícula en el momento en que se separa de la esfera. Esta posición es

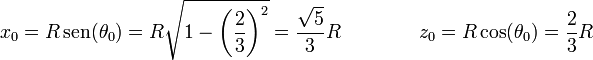
$x_0 = R\,\mathrm{sen}(\theta_0) = R\sqrt{1-\left(\frac{2}{3}\right)^2}=\frac{\sqrt{5}}{3}R\qquad\qquad z_0 = R\cos(\theta_0)=\frac{2}{3}R$

Para la velocidad conocemos ya su módulo

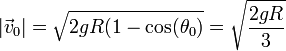
$|\vec{v}_0|=\sqrt{2gR(1-\cos(\theta_0)}=\sqrt{\frac{2gR}{3}}$

y su dirección la da el vector tangente a la esfera en el punto de separación

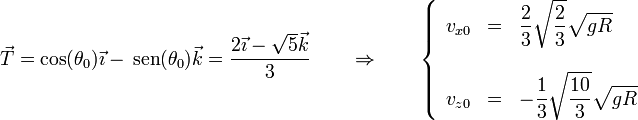
$\vec{T}=\cos(\theta_0)\vec{\imath}-\,\mathrm{sen}(\theta_0)\vec{k}=\frac{2\vec{\imath}-\sqrt{5}\vec{k}}{3}\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}v_{x0} & = & \displaystyle \frac{2}{3}\sqrt{\frac{2}{3}}\sqrt{gR}\\ && \\ v_{z0} & = & \displaystyle -\frac{1}{3}\sqrt{\frac{10}{3}}\sqrt{gR}\end{array}\right.$

Llevando esto a las ecuaciones horarias queda

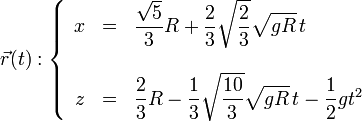
$\vec{r}(t):\left\{\begin{array}{rcl} x & = & \displaystyle \frac{\sqrt{5}}{3}R + \frac{2}{3}\sqrt{\frac{2}{3}}\sqrt{gR}\,t \\ && \\ z & = & \displaystyle \frac{2}{3}R-\frac{1}{3}\sqrt{\frac{10}{3}}\sqrt{gR}\,t-\frac{1}{2}gt^2\end{array}\right.$

El punto de impacto corresponde a que la altura iguale a la del suelo

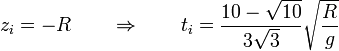
$z_i=-R\qquad \Rightarrow\qquad t_i = \frac{10-\sqrt{10}}{3\sqrt{3}}\sqrt{\frac{R}{g}}$

y sustituyendo en la ecuación para la coordenada x obtenemos el punto de impacto

$x_i = \frac{5}{27}\left(4\sqrt{2}+\sqrt{5}\right)R = 1.461 R\qquad\qquad z_i = -R$

Partícula que se despega de esfera

De Laplace

Contenido

1 Enunciado

2 Punto de separación

3 Rapidez de impacto

4 Punto de impacto

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES