5.10. Hélice de avión en rotación
De Laplace
Revisión a fecha de 19:25 8 dic 2010; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
El avión (sólido “0”) de la figura se mueve de modo que el centro C de su hélice describe una circunferencia de radio L. El módulo de la velocidad angular de este giro es constante y su módulo es 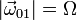 . Además, la hélice (sólido “2”), cuyo radio es R, gira en torno a un eje perpendicular a ella y que pasa por su centro, con velocidad angular también de módulo constante
. Además, la hélice (sólido “2”), cuyo radio es R, gira en torno a un eje perpendicular a ella y que pasa por su centro, con velocidad angular también de módulo constante 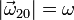 . Se pide
. Se pide
- La reducción cinemática de los movimientos {01} y {20}.
- Aplicando la composición de velocidades, la velocidad
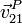 y aceleración
y aceleración 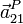 del punto más alto de la hélice (punto P en la figura).
del punto más alto de la hélice (punto P en la figura).
- La reducción cinemática del movimiento {21} en P y la ecuación de su EIRMD ¿Qué tipo de movimiento describe la hélice respecto al sólido “1”?
- Calcule numéricamente
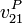 y
y 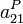 para los valores
para los valores 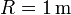 ,
, 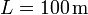 ,
, 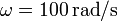 y
y 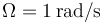 .
.
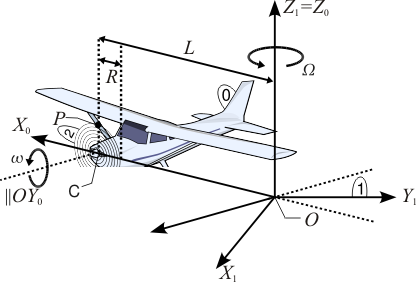
Nota: Se recomienda utilizar el triedro asociado al sólido “0” para resolver el problema.





