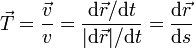Independencia de la parametrización
De Laplace
Contenido |
1 Introducción
A la hora de estudiar la cinemática de la partícula, surgen conceptos puramente geométricos que no dependen de la ley horaria del movimiento de una partícula (esto es, de con qué celeridad pasa de un punto a otro). Otros, en cambio, sí dependen. Por ejemplo, la velocidad instantánea es claramente dependiente del estado de movimiento. Sin embargo, el vector tangente a la trayectoria, que nos indica hacia donde se dirige la partícula, y que se calcula a partir de la velocidad instantánea, no depende de si la partícula se mueve lento o rápido. La dirección del movimiento es una propiedad geométrica.
Si lo que tenemos es un movimiento, dado por su ecuación horaria 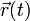 , ¿cómo podemos saber si una propiedad concreta, calculada a partir de ella, es una propiedad geométrica o es dependiente del estado de movimiento?
, ¿cómo podemos saber si una propiedad concreta, calculada a partir de ella, es una propiedad geométrica o es dependiente del estado de movimiento?
La respuesta es que hay que establecer si dicha propiedad es independiente de la parametrización. Esto es, nos imaginamos que la partícula recorre los mismos puntos a un ritmo diferente, de forma que la ecuación horaria es ahora 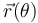 , siendo θ una nueva variable temporal. Si calculando la propiedad empleando la nueva variable resulta el mismo valor que con la original, entonces es una propiedad geométrica, esto es, no depende de cómo de rápido se recorre la curva.
, siendo θ una nueva variable temporal. Si calculando la propiedad empleando la nueva variable resulta el mismo valor que con la original, entonces es una propiedad geométrica, esto es, no depende de cómo de rápido se recorre la curva.
Por ejemplo, nos imaginamos un transportista que hace regularmente el camino Sevilla-Madrid. Sale todos los días de Sevilla a las 7:00 pero cada día para en estaciones de servicio diferentes, por lo que si un día pasa por Córdoba a las 8:15 (este sería el valor de t) otro día pasa por la misma ciudad a las 8:45 (este sería el valor de θ). ¿Cambia la distancia Sevilla-Córdoba por el hecho de la diferente hora de llegada? No. Por tanto es una propiedad geométrica, independiente de la parametrización. ¿Cambia la velocidad media en el trayecto Sevilla-Córdoba? Sí. Por tanto, la velocidad media no es una propiedad geométrica.
Alternativamente, una propiedad que puede calcularse a partir de otras propiedades geométricas es también geométrica. Por ello, otro procedimiento consiste en relacionar las nuevas magnitudes con las previamente conocidas.
En lo que sigue indicaremos las principales propiedades geométricas que aparecen en la cinemática de la partícula.
2 Trayectoria
La trayectoria es, por definición, una propiedad geométrica, independiente de la celeridad.
Se define como el conjunto de puntos del espacio por los que pasa la partícula en su movimiento. Puesto que para analizar la dependencia con el estado de movimiento debemos suponer que se recorren los mismos puntos a ritmo diferente, es inmediato que el conjunto de todos los puntos, que forman la trayectoria, es el mismo para todas las posibles celeridades.
3 Desplazamiento diferencial
El desplazamiento diferencial 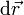 , vector que une dos puntos vecinos a lo largo de la trayectoria, es también una propiedad geométrica, pues la posición de estos puntos vecinos no se ve afectada por la rapidez.
, vector que une dos puntos vecinos a lo largo de la trayectoria, es también una propiedad geométrica, pues la posición de estos puntos vecinos no se ve afectada por la rapidez.
4 Parámetro arco
El parámetro arco o parámetro natural es la distancia medida a lo largo de la trayectoria. Se define mediante la relación diferencial
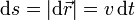
Puesto que el desplazamiento diferencial es una propiedad geométrica, su módulo también lo es. Por tanto, el parámetro arco es independiente de la parametrización.
En forma integral el parámetro natural viene dado por la integral
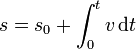
Si en vez de el tiempo del movimiento real de una partícula empleamos cualquier otra variable para describir la curva, el parámetro arco se calculará con la expresión correspondiente
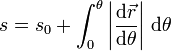
5 Vector tangente
El vector tangente a la curva se calcula normalizando la velocidad