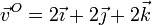Ejemplo de diferentes estados de movimiento
De Laplace
Revisión a fecha de 10:38 6 ago 2010; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
Los vectores de posición y las velocidades de tres puntos de un sólido son, en el SI,
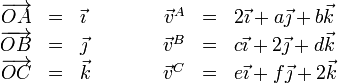
- ¿Qué restricciones impone la condición de rigidez a los valores de las incógnitas a, b, c, d, e y f?
- Halle la velocidad del origen de coordenadas,
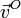 .
.
- Halle los valores de estos parámetros si el sólido se encuentra en un estado de traslación instantáneo.
- Establezca la condición que deben cumplir las constantes si el estado de movimiento es una rotación pura. En este caso, halle el valor de la velocidad angular y la posición del eje instantáneo de rotación.
- En el caso de un estado de movimiento helicoidal, halle la velocidad angular, la velocidad de deslizamiento y la posición del eje instantáneo de rotación y mínimo deslizamiento.
- Para los casos siguientes de los valores de los parámetros
| Caso | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| (a) | 2 | 4 | 2 | 4 | 0 | 0 |
| (b) | 1 | 2 | 3 | 0 | 2 | 4 |
| (c) | 2 | 2 | 2 | 2 | 2 | 2 |
| (d) | 3 | 0 | 1 | -1 | 4 | 4 |
| (e) | 0 | 1 | 4 | 3 | 3 | 1 |
| (f) | 1 | 2 | 3 | 2 | -1 | 1 |
- Indique cuáles corresponden a movimientos rígidos.
- En los casos rígidos, indique si son estados de traslación, rotación o movimiento helicoidal.
- En los casos de rotación, halle la velocidad angular y el EIR.
- En los casos helicoidales, halle la velocidad angular, la de deslizamiento y la posición del EIRMD.
2 Condición de rigidez
La condición cinemática de rigidez implica la equiproyectividad del campo de velocidades:
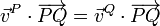
Aplicando esto a cada uno de los pares de puntos del enunciado tenemos, para los puntos A y B
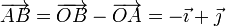
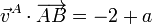
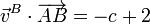

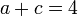
Repitiendo para A y C
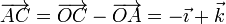
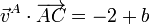
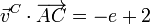

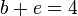
y para B y C
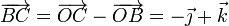
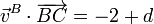
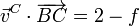

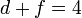
Los parámetros deben cumplir las condiciones
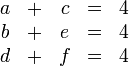
Podemos simplificar la notación haciendo



de manera que las velocidades quedan
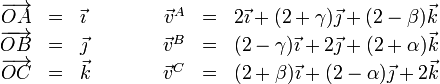
Quedan aun tres parámetros por fijar, que dependerán del estado de movimiento del sólido.
3 Velocidad del origen
La velocidad del origen de coordenadas la obtenemos aplicando la equiproyectividad entre los pares formados por este punto y los tres que conocemos. Si
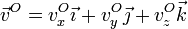
debe cumplirse
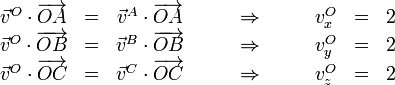
Reuniendo los tres resultados