Partícula que impacta con un muelle

De Laplace

1 Enunciado

Una masa m se encuentra al borde de una pendiente. Después de la pendiente se extiende una llanura, al final de la cual hay un muelle relajado de constante elástica k y longitud natural l₀. La masa se encuentra a una altura h relativa al muelle. Suponemos que no existe fuerza de rozamiento entre la masa y la superficie.

1. Determine la velocidad con la que la masa impacta en el muelle (punto B).
2. ¿Cuál es el valor mínimo de la constante elástica del muelle, k_min, para que este pueda evitar que la masa toque la pared?
3. Suponga ahora que entre los puntos A y B hay una región de longitud d en la que existe rozamiento entre la masa y el suelo. Si el coeficiente de rozamiento es μ, ¿cu´al es el nuevo valor mínimo de k en el apartado anterior?
4. Supongamos que k > k_min. En la situación de rozamiento del apartado anterior, calcule la velocidad con la que la partícula vuelve al punto A y la altura a la que sube por la pendiente.
5. Calcule numéricamente las magnitudes pedidas si 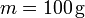, , 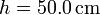, 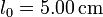μ = 0.200, , .

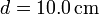2 Velocidad de impacto

3 Constante mínima

4 Constante con rozamiento

5 Altura máxima

6 Valores numéricos