Propulsión a reacción

De Laplace

Revisión a fecha de 16:41 11 feb 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Un cohete a reacción se impulsa en el espacio emitiendo gases a cierta velocidad en el sentido opuesto a su propio movimiento. Sea un cohete que tiene una masa $M 0$ y lleva una carga inicial de combustible $m 0$ . Este combustible es expulsado a ritmo constante 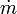$\dot{m}$ con una velocidad constante respecto a la nave, $v 0$ . Si la nave parte del reposo, ¿cuál será su velocidad cuando se le agote el combustible?

2 Solución

Si el cohete se mueve por el espacio libre de fuerzas externas, la cantidad de movimiento del sistema debe conservarse en todo momento. Pero, dado que los gases expulsados se llevan una cierta cantidad de movimiento el resultado es que la cantidad de movimiento del cohete también varía.

Para determinar la velocidad como función del tiempo, establecemos la conservación de la masa y de la cantidad de movimiento entre un instante $t$ y un instante siguiente $t + d t$ .

Si suponemos que los gases son expulsados siempre en la misma dirección en la que se mueve el cohete (aunque si deseara maniobrar debería expulsarlos en una dirección diferente) el problema es unidimensional, por lo que podemos usar cantidades escalares.

En el instante $t$ la cantidad de movimiento del cohete más el combustible que lleva en ese momento es

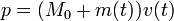
$p = (M_0+ m(t))v(t)\,$

En el instante $t + d t$ la masa de la nave más combustible pasa a ser

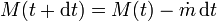
$M(t+\mathrm{d}t) = M(t) - \dot{m}\,\mathrm{d}t$

mientras que su velocidad pasa a ser

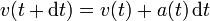
$v(t+\mathrm{d}t)=v(t)+a(t)\,\mathrm{d}t\,$

La cantidad de gas expulsada es

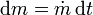
$\mathrm{d}m = \dot{m}\,\mathrm{d}t$

y la velocidad con la que se mueve este gas no es $v 0$ , ya que esta es la velocidad con la que sale expulsado respecto a la nave. La velocidad del gas, para un observador exterior es

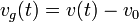
$v_g(t) = v(t) - v_0\,$

Aplicando ahora la ley de conservación de la cantidad de movimiento queda

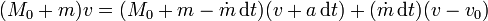
$(M_0+m)v = (M_0+m - \dot{m}\,\mathrm{d}t)(v + a\,\mathrm{d}t) + (\dot{m}\,\mathrm{d}t)(v-v_0)$

Desarrollando y eliminado los términos que quedan a ambos lados resulta, tras simplificar

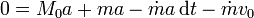
$0 = M_0a+ma-\dot{m}a\,\mathrm{d}t -\dot{m}v_0$

El término proporcional a \mathrm{d}t es despreciable, con lo que llegamos finalmente a la relación

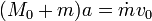
$(M_0+m)a = \dot{m}v_0\,$

Aquí $m$ no es una constante, sino que

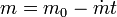
$m = m_0-\dot{m}t$

Para obtener la velocidad como función del tiempo, despejamos la aceleración

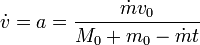
$\dot{v}= a = \frac{\dot{m}v_0}{M_0+m_0-\dot{m}t}$

Integrando entre $t = 0$ y 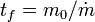$t_f = m_0/\dot{m}$ (cuando $m$ se hace 0) obtenemos la velocidad final

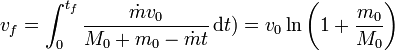
$v_f = \int_0^{t_f} \frac{\dot{m}v_0}{M_0+m_0-\dot{m}t}\,\mathrm{d}t ) = v_0\ln\left(1+\frac{m_0}{M_0}\right)$

Esta fórmula hay que corregirla para el caso de que se alcancen grandes velocidades o en lugar de gases se emita energía pura (como luz), en cuyo caso hay que usar cálculos relativistas.

Propulsión a reacción

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES