Entropía

De Laplace

Revisión a fecha de 17:48 16 may 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Introducción

2 Desigualdad de Clausius

La desigualdad de Clausius establece que, para todo proceso cíclico

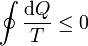
$\oint\frac{\mathrm{d}Q}{T}\leq 0$

donde cada uno de los símbolos posee la siguiente interpretación

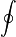
$\oint$: La integral con el circulito se denomina “integral cerrada” y quiere decir que la suma se efectúa sobre una curva que se cierra sobre sí misma

$d Q$: representa la cantidad de calor diferencial que entra en el sistema desde un foco situado a la temperatura $T$ . A lo largo de un ciclo habrá ocasiones en que su valor sea positivo y veces en que será negativo, según el sistema absorba o ceda calor.

$T$: es la temperatura del foco que cede el calor. No es la temperatura del sistema. Es más, para empezar la temperatura del sistema probablemente ni estará definida. En algunos puntos tendrá un valor y en otros será distinto. En el caso de que sí tenga un valor definido, $T'$ , este valor será menor que el exterior cuando el calor entra (ya que si no, no entraría), y será mayor que el exterior cuando el calor sale. Solo en un proceso reversible $T'$ se diferenciará una cantidad infinitesimal de $T$ (ya que si no, no sería reversible).

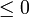
$\leq 0$: La desigualdad de Clausius no nos dice cuanto vale la integral, en general. Solo nos informa de sus signo. Pero al hacerlo nos proporciona un criterio para clasificar los posibles procesos:

Si la integral es negativa: el proceso es irreversible.

Si la integral es nula: el proceso es reversible.

Si la integral es positiva: el proceso es imposible.

3 Definición de entropía

3.1 Variación de entropía

Para un ciclo reversible, la desigualdad de Clausius se transforma en una igualdad.

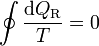$\oint\frac{\mathrm{d}Q_\mathrm{R}}{T}= 0$ (ciclo reversible)

Consideremos ahora un ciclo reversible que pasa por dos estados A y B. Podemos suponer este ciclo como formado por dos caminos $C$ y $C'$ que van de A a B, siendo uno de ellos ( $C'$ ) recorrido de B a A. Para este ciclo la igualdad se convierte en

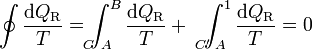
$\oint\frac{\mathrm{d}Q_\mathrm{R}}{T}=\int_{A\!\!\!\!\!\!\!\!\!\!\!\!C}^B\frac{\mathrm{d}Q_\mathrm{R}}{T}+\ \ \int_{A\!\!\!\!\!\!\!\!\!\!\!\!\!C'}^1\frac{\mathrm{d}Q_\mathrm{R}}{T}=0$

y, despejando

$\int_{A\!\!\!\!\!\!\!\!\!\!\!\!C}^B\frac{\mathrm{d}Q_\mathrm{R}}{T}=-\ \ \int_{B\!\!\!\!\!\!\!\!\!\!\!\!\!C'}^A\frac{\mathrm{d}Q_\mathrm{R}}{T}=0$

Ahora bien, por ser los caminos reversibles, la integral de B a A por C' es igual a la integral de A a B por el mismo camino C', cambiada de signo. Físicamente, esto quiere decir que si vamos de B a A por C' y en un cierto paso entra en el sistema una cantidad de calor $d Q R$ , si recorremos el camino en sentido contrario, cuando lleguemos al mismo sitio la misma cantidad de calor saldrá del sistema (es decir, que en el camino inverso entra $- d Q R$ ). Por tanto

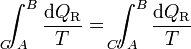
$\int_{A\!\!\!\!\!\!\!\!\!\!\!\!C}^B\frac{\mathrm{d}Q_\mathrm{R}}{T} =\ \int_{A\!\!\!\!\!\!\!\!\!\!\!\!\!C'}^B\frac{\mathrm{d}Q_\mathrm{R}}{T}$

Puesto que este resultado puede extenderse a cualquier otro camino reversible que conecte A con B, concluimos que el valor de la integral es independiente del camino y por tanto solo depende de los estados inicial y final. Por ello, su valor es igual a la diferencia de una cierta función de estado que denominamos entropía

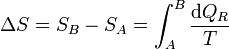
$\Delta S = S_B - S_A = \int_A^B \frac{\mathrm{d}Q_R}{T}$

o, en forma diferencial

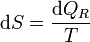
$\mathrm{d}S = \frac{\mathrm{d}Q_R}{T}$

Dicho con palabras: el incremento diferencial de entropía entre dos estados vecinos es igual la cantidad de calor que entra reversiblemente entre dichos estados dividida por la temperatura a la que se intercambia el calor. Puesto que estamos hablando de procesos reversibles no es necesario distinguir entre la temperatura del ambiente T y la del sistema T', ya que en un proceso reversible ambas deben diferenciarse como mucho en una cantidad infinitesimal.

De la definición de la entropía se ve que sus unidades en el sistema internacional son el J/K.

3.2 Entropía absoluta

La definición anterior sólo nos da la diferencia de entropía entre dos estados, no su valor absoluto. Es más, hemos afirmado, sin probarlo, que el resultado de la integral es una diferencia de los valores de la entropía en B y en A. ¿Por qué la diferencia y no, por ejemplo, el cociente $f (B) / f (A)$ ?

Podemos definir la entropía respecto a un cierto estado de referencia, O, como la integral

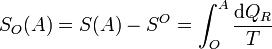
$S_O(A) = S(A)-S^O = \int_O^A \frac{\mathrm{d}Q_R}{T}$

Este estado O, por definición, tendrá entropía nula respecto a sí mismo ( $S O (O) = 0$ ). Puesto que O es un estado fijo, esta integral solo depende de A.

Consideremos ahora la integral entre A y B

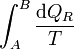
$\int_A^B \frac{\mathrm{d}Q_R}{T}$

Puesto que podemos elegir el camino que queramos para ir de A a B, tomamos uno que pase por O. Entonces

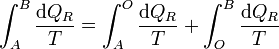
$\int_A^B \frac{\mathrm{d}Q_R}{T}=\int_A^O \frac{\mathrm{d}Q_R}{T}+\int_O^B \frac{\mathrm{d}Q_R}{T}$

y puesto que los caminos son reversibles

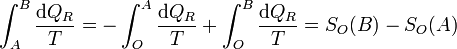
$\int_A^B \frac{\mathrm{d}Q_R}{T}=-\int_O^A \frac{\mathrm{d}Q_R}{T}+\int_O^B \frac{\mathrm{d}Q_R}{T}=S_O(B)-S_O(A)$

Luego efectivamente sí resulta la diferencia entre la función evaluada en B y la misma función evaluada en A.

Realmente esta definición lo que nos da es de nuevo una diferencia, pero respecto a un estado estándar, que puede ser establecido por convenio. La IUPAC recomienda definir el estado estándar como el correspondiente a una presión de 100 kPa (0.9869 atm) y 0°C (aunque la mayoría de las tablas dan la entropía del estado estandar a 25°C).

El cambio de estado de referencia lo que añade es una constante a la entropía. Por ello, si lo que queremos calcular es la variación de entropía entre dos estados A y B, nos es indiferente el estado de referencia que tomemos, nos basta con hacer la integral directamente por un camino reversible que vaya de A a B.

Cuando se formula el Tercer Principio de la termodinámica, que establece que la entropía de un cristal perfecto, a 0 K es nula, se da un verdadero valor absoluto a la entropía, pues fija un estado de referencia universal.

4 Principio del aumento de entropía

4.1 Ciclo parcialmente irreversible

Supongamos ahora un ciclo irreversible formado por un camino irreversible que lleva del estado A al B y vuelve por un camino reversible. En este caso tenemos la desigualdad

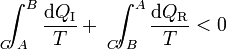
$\int_{A\!\!\!\!\!\!\!\!\!\!\!\!C}^B\frac{\mathrm{d}Q_\mathrm{I}}{T}+\ \ \int_{B\!\!\!\!\!\!\!\!\!\!\!\!\!C'}^A\frac{\mathrm{d}Q_\mathrm{R}}{T}<0$

Cambiando uno de los términos de miembro

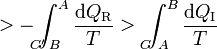
$>-\int_{B\!\!\!\!\!\!\!\!\!\!\!\!\!C'}^A\frac{\mathrm{d}Q_\mathrm{R}}{T}>\ \int_{A\!\!\!\!\!\!\!\!\!\!\!\!C}^B\frac{\mathrm{d}Q_\mathrm{I}}{T}$

A la integral sobre el camino reversible podemos invertirla y cambiarle el signo (cosa que no podemos con el irreversible, precisamente por ser irreversible). Por tanto la desigualdad anterior equivale a decir que la integral por el camino reversible es mayor que por el irreversible

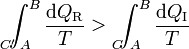
$\int_{A\!\!\!\!\!\!\!\!\!\!\!\!\!C'}^B\frac{\mathrm{d}Q_\mathrm{R}}{T} >\ \int_{A\!\!\!\!\!\!\!\!\!\!\!\!C}^B\frac{\mathrm{d}Q_\mathrm{I}}{T}$

Pero la integral por el camino reversible es justamente la diferencia entre la entropía inicial y la final. Por tanto

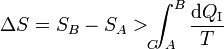
$\Delta S = S_B -S_A > \int_{A\!\!\!\!\!\!\!\!\!\!\!\!C}^B\frac{\mathrm{d}Q_\mathrm{I}}{T}$

Combinando este resultado con el del caso reversible obtenemos la relación general

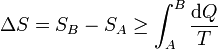
$\Delta S = S_B -S_A \ge \int_{A}^B\frac{\mathrm{d}Q}{T}$

La variación de la entropía es siempre mayor o igual que la integral del calor que entra en el sistema dividido por la temperatura a la que entra. La igualdad se dará en un proceso reversible y la desigualdad en uno irreversible.

4.2 Principio del aumento de entropía

En el caso particular de un sistema aislado, ningún calor entra o sale del sistema, $d Q = 0$ y por tanto

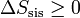$\Delta S_\mathrm{sis} \geq 0$ (sistema aislado)

esto es, para un sistema aislado la entropía es una función creciente en todo proceso real. Sólo si el proceso es reversible la entropía permanece constante.

Si consideramos el “universo” como el conjunto del sistema más la parte del ambiente con la que intercambia calor o trabajo, podemos tratar al universo como un sistema aislado, con lo que obtenemos el principio del aumento de entropía:

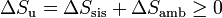
$\Delta S_\mathrm{u}=\Delta S_\mathrm{sis}+\Delta S_\mathrm{amb}\geq 0$

esto es, en todo proceso real la entropía aumenta (si el proceso es irreversible) o permanece estacionaria (si es reversible), pero nunca disminuye.

Obsérvese que en un proceso real es posible que la entropía del sistema disminuya (es lo que ocurre normalmente si se enfría), pero esa disminución debe ser compensada por un aumento en el ambiente, que supere con creces dicha disminución.

5 Producción de entropía

La desigualdad de Clausius en términos de la entropía

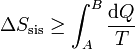
$\Delta S_\mathrm{sis} \geq \int_A^B\frac{\mathrm{d}Q}{T}$

puede convertirse en una igualdad introduciendo un nuevo término

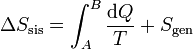
$\Delta S_\mathrm{sis} = \int_A^B\frac{\mathrm{d}Q}{T}+S_\mathrm{gen}$

donde $S gen$ es la producción de entropía. Representa la cantidad de entropía producida en el sistema como consecuencia de las irreversibilidades internas. La desigualdad de Clausius establece, por tanto, el criterio

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): S_\gen=\begin{cases} > 0 & \mbox{proceso irreversible} \\ = 0 & \mbox{proceso reversible} \\ & \mbox{proceso imposible}\end{cases}

Escrita la desigualdad de esta forma podemos entender la variación de entropía como suma de dos términos: lo que entra por las paredes debido al calor intercambiado con el ambiente más lo que se produce en el propio sistema.

Otra forma de interpretarlo es escribiendo la igualdad anterior como

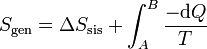
$S_\mathrm{gen}=\Delta S_\mathrm{sis} + \int_A^B\frac{-\mathrm{d}Q}{T}$

Como se ve más abajo, la variación de entropía de un foco es $Q / T$ , siendo $Q$ el calor que entra en el foco. En la integral anterior $- d Q$ es la cantidad de calor que sale del sistema y por tanto entra en el foco a temperatura $T$ . Al sumar para todos los focos estamos calculando la variación total de entropía del ambiente, Nos queda entonces

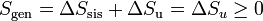
$S_\mathrm{gen}=\Delta S_\mathrm{sis} + \Delta S_\mathrm{u}=\Delta S_u \ge 0$

con lo que la entropía generada en el sistema y la variación de entropía del universo son cantidades equivalentes.

6 Variación de entropía en una máquina térmica

6.1 Variación de entropía de un foco térmico

En el caso particular de un foco térmico su capacidad calorífica es tan grande que la entrada o salida en él no produce un aunmento o disminución de su temperatura. Esto quiere decir que el intercambio de calor con un foco es siempre un proceso reversible (desde el punto de vista del foco), por lo que la variación de entropía del foco es simplemente

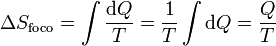
$\Delta S_\mathrm{foco}=\int \frac{\mathrm{d}Q}{T}=\frac{1}{T}\int \mathrm{d}Q=\frac{Q}{T}$

Aquí $Q$ es el calor que entra en el foco (que normalmente saldrá del sistema).

6.2 Variación en un ciclo de la máquina

Cuando tenemos una máquina térmica que intercambia calor con dos focos a temperatura $T c$ y $T f$ , la variación de entropía del universo será la suma de la de la máquina más la del ambiente.

6.2.1 Del sistema

La máquina realiza un proceso cíclico. Puesto que la entropía es una función de estado su valor al final del ciclo será el mismo que al principio. Por tanto

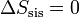$\Delta S_\mathrm{sis}=0\,$ (proceso cíclico)

6.2.2 Del ambiente

La máquina intercambia calor con dos focos térmicos. Del foco a $T c$ sale una cantidad de calor $| Q c |$ . En el foco a $T f$ entra un calor $| Q f |$ . Por tanto la variación de entropía del ambiente es

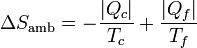
$\Delta S_\mathrm{amb}=-\frac{|Q_c|}{T_c}+\frac{|Q_f|}{T_f}$

6.2.3 Del universo

Puesto que la entropía del sistema no cambia en un ciclo, la variación de entropía del universo coincide con la del ambiente

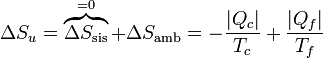
$\Delta S_u=\overbrace{\Delta S_\mathrm{sis}}^{=0}+\Delta S_\mathrm{amb}=-\frac{|Q_c|}{T_c}+\frac{|Q_f|}{T_f}$

Para que esta máquina pueda operar, esta variación de entropía debe ser positiva. La reducción de entropía del primer foco debe ser compensada con creces por el aumento en el otro. Este criterio limita la eficiencia de máquinas térmicas y refrigeradores.

7 Relación con otros enunciados del segundo principio

8 Entropía y trabajo perdido

9 Ejemplos

9.1 Máquina térmica

9.2 Inmersión en un baño térmico

9.3 Cambio de fase

9.4 Gas ideal

9.5 Mezcla de gases

9.6 Reacciones químicas

Cuando se analiza una reacción química lo que se suele hacer es

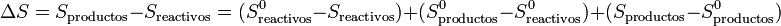
$\Delta S = S_\mathrm{productos}-S_\mathrm{reactivos}= (S^0_\mathrm{reactivos}-S_\mathrm{reactivos})+(S_\mathrm{productos}^0-S_\mathrm{reactivos}^0)+(S_\mathrm{productos}-S_\mathrm{productos}^0)$

siendo $S 0$ las entropías medidas y tabuladas en el estado estándar (normalmente a 100 kPa y 298 K). La segunda diferencia representa la variación de la entropía en la reacción en el estado estándar

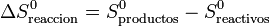
$\Delta S^0_\mathrm{reaccion}=S_\mathrm{productos}^0-S_\mathrm{reactivos}^0$

Lo que quiere decir esta descomposición en tres sumas es que, para estudiar una reacción a una cierta presión y temperatura, aprovechamos el que la entropía es una función de estado. En lugar de calcular la diferencia directamente a dicha $p$ y $T$ , lo que hacemos es imaginarnos que llevamos los reactivos, sin reaccionar, al estado estándar. Luego analizamos la reacción en el estado estándar, aprovechando los valores tabulados. Por último llevamos los productos al estado original.

10 Entropía y exergía