Test del primer parcial 2019-2020 (GIOI)
De Laplace
Contenido |
1 Aceleración a trozos
Una partícula se mueve en un movimiento rectilíneo que parte del reposo en x = 0. Durante un intervalo T se mueve con aceleración constante a0. A partir de ahí se mueve con aceleración constante − a0 / 2 durante un intervalo 2T.
1.1 Pregunta 1
¿Cuánto vale la velocidad de la partícula en t = 3T?
- A − a0T.
- B a0T.
- C 0.
- D a0T / 2.
- Solución
La respuesta correcta es la C.
1.2 Pregunta 2
¿Cuál es el desplazamiento de la partícula entre t = 0 y t = 3T?
- A − 3a0T2 / 2.
- B 3a0T2 / 2.
- C 0.
- D − a0T2.
- Solución
La respuesta correcta es la B.
2 Cambio en la velocidad
En un movimiento en el plano OXY, la velocidad de una partícula en un instante dado es 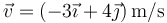 y su aceleración en ese mismo instante es
y su aceleración en ese mismo instante es  .
.
2.1 Pregunta 1
En este instante la partícula está…
- A ni frenando ni acelerando. Su rapidez es constante.
- B frenando.
- C acelerando.
- D No hay información suficiente para saber si acelera o frena.
- Solución
La respuesta correcta es la B.
2.2 Pregunta 2
En ese instante y, mirando desde el eje OZ positivo, la partícula…
- A está desviándose hacia su izquierda.
- B no se desvía, sino que avanza en línea recta.
- C está desviándose hacia su derecha.
- D No hay información suficiente para saber si cambia de dirección.
- Solución
La respuesta correcta es la C.
3 Producto escalar y vectorial
Sean  y
y  dos vectores no nulos. Indique en qué caso se cumple la igualdad
dos vectores no nulos. Indique en qué caso se cumple la igualdad
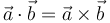
- A Cuando
 y
y  son paralelos.
son paralelos.
- B Cuando
 y
y  son perpendiculares.
son perpendiculares.
- C Cuando
 y
y  forman un ángulo de 45°.
forman un ángulo de 45°.
- D Nunca.
- A Cuando
- Solución
La respuesta correcta es la D.





