Péndulo Compuesto (I) (CMR)
De Laplace
Contenido |
1 Enunciado
Se tiene un péndulo compuesto consistente en una barra homogénea de longitud 2b y masa m suspendida por un punto situado O a una distancia d del centro G de la barra (d < b).:
- Determine el periodo de oscilación de la barra si se suelta desde un ángulo pequeño θ0 respecto a la vertical.
- Suponga ahora que la barra se sitúa en el equilibrio inestable con el CM por encima del punto de apoyo y desde ahí se suelta con una velocidad inicial muy pequeña. Para el instante en que pasa por la vertical, calcule:
- La velocidad angular de la barra y la velocidad lineal de los extremos de la barra.
- Calcule la fuerza ejercida sobre el punto de anclaje.
- Calcule la tensión en cada punto de la barra.
- Repita los cálculos del apartado anterior para el momento en que forma un ángulo θ con la vertical.
2 Ecuación de movimiento
2.1 A partir de la energía
Al ser un sistema con un solo grado de libertad (el ángulo que forma con la vertical), podemos determinar la ecuación de movimiento a partir de la energía mecánica, que e suna cantidad constante al ser un sistema conservativo
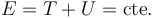
La energía cinética es la correspondiente a una rotación respectoa un punto fijo O
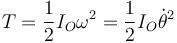
siendo el momento de inercia, de acuerdo con el teorema de Steiner
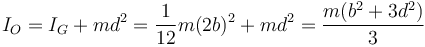
La energía potencial, tomando como referencia el punto O, es la correspondiente al peso. La posición vertical del CM es zG = − dcos(θ), por lo que
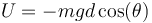
Esto da la energía mecánica
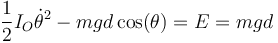
El valor de la constante sale de que la posición inicial es vertical y hacia arriba (θ = π) en reposo.
Como esta cantidad es constante, su derivada respecto al tiempo se anula
0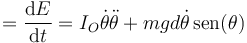
Sacando factor común
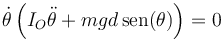
lo que nos da la ecuación de movimiento
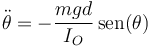
2.2 A partir de fuerzas y momentos
Un método más sistemático, que no depende de si el sistema es conservativo o no, o de si tiene uno o más grados de libertad, consiste en usar las ecuaciones de Newton y Euler para la traslación y la rotación.
De acuerdo con la segunda ley de Newton
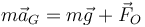
siendo 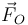 la fuerza de reacción en el soporte. Esta fuerza es desconocida de antemano, por lo que esta ecuación no es suficiente para determinar la ecuación de movimiento. De hecho, la emplearemos más tarde para calcular esta fuerza de reacción.
la fuerza de reacción en el soporte. Esta fuerza es desconocida de antemano, por lo que esta ecuación no es suficiente para determinar la ecuación de movimiento. De hecho, la emplearemos más tarde para calcular esta fuerza de reacción.
La ecuación de Euler para la rotación es
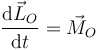
siendo el momento aplicado
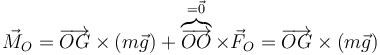
Vemos que al reducir el problema en el punto O eliminamos el momento debido a la fuerza de reacción.
El único momento es el del peso, que es igual a
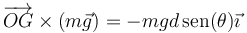
Aquí hemos tomado un sistema de ejes en el que el OZ es vertical, el péndulo oscila en el plano OYZ y por tanto el eje OX es el normal al plano hacia afuera. Para un ángulo θ > 0 el par produce un giro en torno a OX pero en sentido horario (negativo). Su módulo es igual al módulo del primero (d) por el módulo del segundo (mg) por el seno del ángulo que forman.
El momento cinético  lo calculamos observando que se trata de una rotación respecto a un eje fijo (OX), que además es un eje principal
lo calculamos observando que se trata de una rotación respecto a un eje fijo (OX), que además es un eje principal
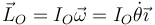
Derivamos aquí respecto al tiempo
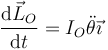
e igualamos al momento de las fuerzas, resultando de nuevo
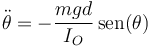
Una vez que tenemos esta ecuación, podemos determinar, si lo deseamos, la fuerza en el soporte como