Colisión con rozamiento

De Laplace

Enunciado

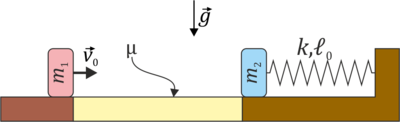
Sobre una superficie horizontal se encuentran dos masas. La masa 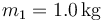se encuentra inicialmente en 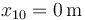y la masa 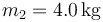en 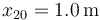. La masa 2 está unida a un resorte de constante 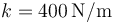y longitud en reposo 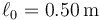, estando inicialmente en la posición de equilibrio. El tramo de 1m entre la masa 1 y la 2 es una superficie rugosa, en la que la constante de rozamiento vale μ = 0.45. El resto de la superficie está pulido.

Estando las dos masas en reposo se le aplica una percusión a la masa 1 de forma que esta adquiere una velocidad inicial v_0=5\,m/s

1. Determine la velocidad de m_1 justo antes de impactar con la masa 2.
2. Calcule las velocidades de ambas masas justo tras el impacto. Suponga que la colisión es perfectamente elástica.
3. Halle la posición x_1f en la que se detiene la masa 1, si llega a hacerlo. Si no se detiene, halle la velocidad con la que llega a su posición inicial.
4. Halle la posición x_2f en la que se detiene m_2 por primera vez.

Tómese 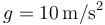.