Test del segundo parcial 2017-2018 (GIE)
De Laplace
Contenido |
1 Cuerpo en plano inclinado
Un cuerpo de 13 N de peso se encuentra sobre la superficie de un plano inclinado de pendiente tg(β) = 5 / 12. El coeficiente de rozamiento del cuerpo con el plano vale μ=0.5. Desde la parte de abajo del cuerpo se le aplica una fuerza de 4 N, tangente al plano y en sentido ascendente.
¿Cuánto vale, en módulo, la fuerza de rozamiento que experimenta el cuerpo?
- A 1 N.
- B 5 N.
- C 6 N.
- D 4 N.
- Solución
La respuesta correcta es la A.
2 Polea con hilos tensos
Dos masas del mismo peso, 10N, están unidas por un hilo ideal (“1”), inextensible y sin masa, que pasa por una polea ideal, sin masa ni rozamiento. Una de las masas está unida al suelo por un resorte de constante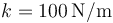 
y longitud natural 
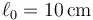. La otra se mantiene a la misma altura que la primera mediante otro hilo ideal (“2”) de 15cm de longitud. ¿Cuánto vale la tensión de cada hilo?
- A
, 
.
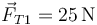- B
, .
- C
, 
.
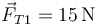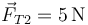- D
, 
.
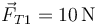- A
- Solución
La respuesta correcta es la C.
3 Fuerza central
Una partícula se mueve por el espacio sometida exclusivamente a la acción de una fuerza central con centro O. ¿Qué magnitudes son constantes de movimiento para esta partícula?
- A Su energía mecánica y su momento cinético respecto a O, pero no su cantidad de movimiento.
- B Su energía mecánica, su momento cinético respecto a O y su cantidad de movimiento.
- C Su energía mecánica, pero no su cantidad de movimiento ni su momento cinético respecto a O.
- D Su energía cinética, su momento cinético respecto a O y su cantidad de movimiento.
- Solución
La respuesta correcta es la A.
4 Radio de curvatura
De la segunda ley de Newton se deduce que, en un movimiento circular uniforme, a igualdad de fuerza y de rapidez, el radio de curvatura…
- A es inversamente proporcional a la masa.
- B es independiente de la masa.
- C es proporcional a la masa.
- D es proporcional a la raíz cuadrada de la masa.
- Solución
La respuesta correcta es la C.
5 Sistema de partículas
Se tiene un sistema de tres partículas, A, B y C, sometidas exclusivamente a fuerzas internas newtonianas. Sus posiciones respectivas son 
, 
y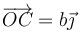 
. La fuerza neta que experimenta la partícula A vale No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{F}_A=F_0\left(2\vec{\imath}-\vec{\jmath})
y la que experimenta la partícula C vale No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{F}_C=F_0\left(-\vec{\imath}+2\vec{\jmath})
.
5.1 Pregunta 1
¿Cuánto vale la fuerza neta sobre la partícula B?
- A No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{F}_B=F_0\left(-\vec{\imath}-\vec{\jmath})
.
- B No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{F}_B=F_0\left(3\vec{\imath}-3\vec{\jmath})
.
- C No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{F}_B=F_0\left(\vec{\imath}+\vec{\jmath})
.
- D No hay información suficiente para saberlo.
- Solución
La respuesta correcta es la A.
5.2 Pregunta 2
¿Cuánto vale la fuerza que cada una de las otras dos partículas ejerce sobre la partícula C?
- A
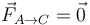, No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{F}_{B\to C}=F_0\left(-\vec{\imath}+2\vec{\jmath})
- A
.
- B
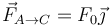, No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{F}_{B\to C}=F_0\left(-\vec{\imath}+\vec{\jmath})
- B
.
- C
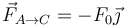, No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{F}_{B\to C}=F_0\left(\vec{\imath}-\vec{\jmath})
- C
.
- D No hay información suficiente para saberlo.
- Solución
La respuesta correcta es la B.
