Test del segundo parcial 2017-2018 (GIE)

De Laplace

Contenido

1 Cuerpo en plano inclinado
2 Polea con hilos tensos
3 Fuerza central
4 Radio de curvatura
5 Sistema de partículas
- 5.1 Pregunta 1
- 5.2 Pregunta 2
6 Oscilador amortiguado
7 El mono y los plátanos

1 Cuerpo en plano inclinado

Un cuerpo de 13 N de peso se encuentra sobre la superficie de un plano inclinado de pendiente $tg(β) = 5 / 12$ . El coeficiente de rozamiento del cuerpo con el plano vale μ=0.5. Desde la parte de abajo del cuerpo se le aplica una fuerza de 4 N, tangente al plano y en sentido ascendente.

¿Cuánto vale, en módulo, la fuerza de rozamiento que experimenta el cuerpo?

A 1 N.
B 5 N.
C 6 N.
D 4 N.

Solución

La respuesta correcta es la A.

La partícula está, en principio en reposo, por tanto se cumple

$m\vec{g}+\vec{F}_n+\vec{F}_r+\vec{F}_\mathrm{apl}=\vec{0}$

Tomamos un sistema de ejes en el que el eje X es tangente a la superficie hacia abajo y el Y es perpendicular a esta, hacia arriba. Si separamos por componentes queda, en la dirección tangencial

$mg\,\mathrm{sen}(\beta)-F_\mathrm{apl}+F_r=0$

siendo

$\mathrm{sen}(\beta)=\frac{5}{\sqrt{5^2+12^2}}=\frac{5}{13}$

lo que da

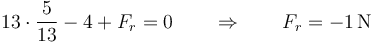
$13\cdot\frac{5}{13}-4+F_r=0\qquad \Rightarrow\qquad F_r=-1\,\mathrm{N}$

el signo menos indica que la fuerza va en sentido opuesto al eje OX, esto es, en sentido ascendente. Dicho en palabras: el peso tira para abajo con 5N, empujamos hacia arriba con 4N, luego queda una fuerza neta de 1N hacia abajo, que es compensada por el rozamiento.

Queda por comprobar si se cumple la condición de rozamiento seco. El equilibrio en la dirección normal da

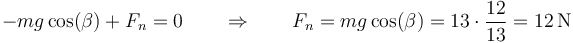
$-mg\cos(\beta)+F_n=0\qquad\Rightarrow\qquad F_n=mg\cos(\beta)=13\cdot\frac{12}{13}=12\,\mathrm{N}$

Debe cumplirse que

$|\vec{F}_r|\leq \mu|\vec{F}_n|\qquad\Rightarrow\qquad 1\,\mathrm{N} \leq 0.5\cdot 12=6\,\mathrm{N}$

Puesto que 1 es menor que 6, que es el máximo rozamiento estático, no hay contradicción, la masa no se mueve y

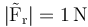
$\mathrm{|\vec{F}_r|=1\,\mathrm{N}}$

2 Polea con hilos tensos

Dos masas del mismo peso, 10N, están unidas por un hilo ideal (“1”), inextensible y sin masa, que pasa por una polea ideal, sin masa ni rozamiento. Una de las masas está unida al suelo por un resorte de constante 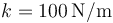$k=100\,\mathrm{N}/\mathrm{m}$ y longitud natural 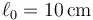$\ell_0=10\,\mathrm{cm}$ . La otra se mantiene a la misma altura que la primera mediante otro hilo ideal (“2”) de 15cm de longitud. ¿Cuánto vale la tensión de cada hilo?

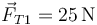A $\vec{F}_{T1}=25\,\mathrm{N}$ , $\vec{F}_{T2}=0\,\mathrm{N}$ .
B $\vec{F}_{T1}=20\,\mathrm{N}$ , $\vec{F}_{T2}=0\,\mathrm{N}$ .
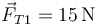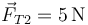C $\vec{F}_{T1}=15\,\mathrm{N}$ , $\vec{F}_{T2}=5\,\mathrm{N}$ .
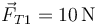D $\vec{F}_{T1}=10\,\mathrm{N}$ , $\vec{F}_{T2}=25\,\mathrm{N}$ .

Solución

La respuesta correcta es la C.

El equilibrio para la masa de la izquierda da

$F_{T1}-mg-F_{T2}=0\,$

y para la de la derecha

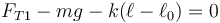
$F_{T1}-mg-k(\ell-\ell_0)=0\,$

La fueza elástica vale, teniendo en cuenta que el muelle mide 15cm

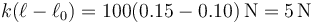
$k(\ell-\ell_0)=100(0.15-0.10)\,\mathrm{N}=5\,\mathrm{N}$

lo que da

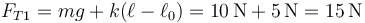
$F_{T1}=mg+k(\ell-\ell_0)=10\,\mathrm{N}+5\,\mathrm{N}=15\,\mathrm{N}$

y

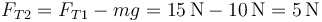
$F_{T2}=F_{T1}-mg=15\,\mathrm{N}-10\,\mathrm{N}=5\,\mathrm{N}$

Dicho en palabras, para que estén en equilibrio a la misma altura, el hilo 2 debe hacer la misma fuerza que el muelle.

3 Fuerza central

Una partícula se mueve por el espacio sometida exclusivamente a la acción de una fuerza central con centro O. ¿Qué magnitudes son constantes de movimiento para esta partícula?

A Su energía mecánica y su momento cinético respecto a O, pero no su cantidad de movimiento.
B Su energía mecánica, su momento cinético respecto a O y su cantidad de movimiento.
C Su energía mecánica, pero no su cantidad de movimiento ni su momento cinético respecto a O.
D Su energía cinética, su momento cinético respecto a O y su cantidad de movimiento.

Solución

La respuesta correcta es la A.

4 Radio de curvatura

De la segunda ley de Newton se deduce que, en un movimiento circular uniforme, a igualdad de fuerza y de rapidez, el radio de curvatura…

A es inversamente proporcional a la masa.
B es independiente de la masa.
C es proporcional a la masa.
D es proporcional a la raíz cuadrada de la masa.

Solución

La respuesta correcta es la C.

Sale de

$|\vec{F}_n|=m\frac{|\vec{v}|^2}{R}\qquad\Rightarrow\qquad R=\left(\frac{|\vec{v}|^2}{|\vec{F}_n|}\right) m$

5 Sistema de partículas

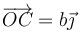Se tiene un sistema de tres partículas, A, B y C, sometidas exclusivamente a fuerzas internas newtonianas. Sus posiciones respectivas son $\overrightarrow{OA}=\vec{0}$ , $\overrightarrow{OB}=b\vec{\imath}$ y $\overrightarrow{OC}=b\vec{\jmath}$ . La fuerza neta que experimenta la partícula A vale $\vec{F}_A=F_0\left(2\vec{\imath}-\vec{\jmath}\right)$ y la que experimenta la partícula C vale $\vec{F}_C=F_0\left(-\vec{\imath}+2\vec{\jmath}\right)$ .

5.1 Pregunta 1

¿Cuánto vale la fuerza neta sobre la partícula B?

A $\vec{F}_B=F_0\left(-\vec{\imath}-\vec{\jmath}\right)$ .
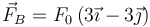B $\vec{F}_B=F_0\left(3\vec{\imath}-3\vec{\jmath}\right)$ .
C $\vec{F}_B=F_0\left(\vec{\imath}+\vec{\jmath}\right)$ .
D No hay información suficiente para saberlo.

Solución

La respuesta correcta es la A.

En un sistema de fuerzas newtonianas, la suma de todas las fuerzas internas debe ser nula.

$\vec{F}_A+\vec{F}_B+\vec{F}_C=\vec{0}\qquad\Rightarrow\qquad \vec{F}_B=-\vec{F}_A-\vec{F}_C$

5.2 Pregunta 2

¿Cuánto vale la fuerza que cada una de las otras dos partículas ejerce sobre la partícula C?

A 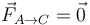$\vec{F}_{A\to C}=\vec{0}$ , $\vec{F}_{B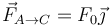\to C}=F_0\left(-\vec{\imath}+2\vec{\jmath}\right)$ .
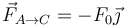B $\vec{F}_{A\to C}=F_0\vec{\jmath}$ , $\vec{F}_{B\to C}=F_0\left(-\vec{\imath}+\vec{\jmath}\right)$ .
C $\vec{F}_{A\to C}=-F_0\vec{\jmath}$ , $\vec{F}_{B\to C}=F_0\left(\vec{\imath}-\vec{\jmath}\right)$ .
D No hay información suficiente para saberlo.

Solución

La respuesta correcta es la B.

En un sistema de fuerzas newtonianas, la fuerzas entre cada par de partículas debe ir en la dirección de la recta que las une

La fuerza sobre C debe tener una componente en la dirección de 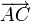$\overrightarrow{AC}$ y otra en la de $\overrightarrow{BC}$ . Por tanto debe ser

$F_0\left(-\vec{\imath}+2\vec{\jmath}\right)=P\vec{\jmath}+Q(-\vec{\imath}+\vec{\jmath})$

Separando por componentes queda

$-F_0=-Q\qquad\qquad 2F_0=P+Q\qquad\rightarrow\qquad Q=F_0\qquad P=F_0$

y las fuerzas

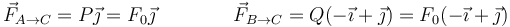
$\vec{F}_{A\to C}=P\vec{\jmath}=F_0\vec{\jmath}\qquad\qquad \vec{F}_{B\to C}=Q(-\vec{\imath}+\vec{\jmath})=F_0(-\vec{\imath}+\vec{\jmath})$

Esto se ve de forma sencilla según el gráfico de arriba.

6 Oscilador amortiguado

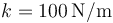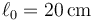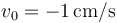Una masa de 1kg está unida a un resorte horizontal de constante $k=100\,\mathrm{N}/\mathrm{m}$ y longitud natural $\ell_0=20\,\mathrm{cm}$ y a un amortiguador de constante $\gamma=40\,\mathrm{N}\cdot\mathrm{s}/\mathrm{m}$ . Estando la masa en su posición de equilibrio se le comunica una velocidad inicial de $v_0=-1\,\mathrm{cm}/\mathrm{s}$ . ¿Cuál de las siguientes figuras representa correctamente la elongación de la masa respecto al tiempo?

A	B


C	D

Solución

La respuesta correcta es la B.

La velocidad inicial (esto es, la pendiente de la tangente a la curva) es negativa y la posición inicial es nula. Esto implica que solo puede ser la A o la B.

Para decidir si es subamortiguado o sobreamortiguado debemos comparar la frecuencia propia y el factor de amortiguamiento. la primera es

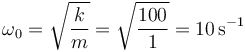
$\omega_0=\sqrt{\frac{k}{m}}=\sqrt{\frac{100}{1}}=10\,\mathrm{s}^{-1}$

y el segundo

$\beta=\frac{\gamma}{2m}=\frac{40}{2\cdot 1}=20\,\mathrm{s}^{-1}$

Como $β > ω 0$ el oscilador es sobreamortiguado, no oscila y la correcta es la B.

7 El mono y los plátanos

Por una polea ideal (sin masa ni rozamiento) pasa una cuerda también ideal. De uno de los extremos del hilo cuelga un racimo de plátanos de 20kg de masa. El extro extremo está libre y en él se halla agarrado un mono también de 20kg. Para coger los plátanos, el mono intenta trepar por la cuerda a la que está agarrado. Cuando lo intenta, ¿qué es lo que ocurre?

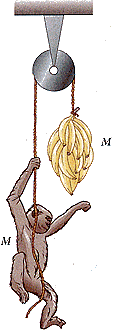
A Los plátanos suben, pero el mono se queda igual o incluso baja.
B Los plátanos se quedan en el mismo sitio, y el mono sube hasta la polea.
C Es físicamente imposible que el mono consiga trepar y los dos se quedan en el mismo sitio.
D Los plátanos y el mono suben los dos al mismo tiempo hasta la polea.

Solución

La respuesta correcta es la D.

La forma más sencilla de resolver este problema es mediante el Teorema del Momento Cinético. Para el punto O, donde está articulada la polea, se cumple que el momento de las fuerzas externas

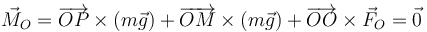
$\vec{M}_O=\overrightarrow{OP}\times(m\vec{g})+\overrightarrow{OM}\times(m\vec{g})+\overrightarrow{OO}\times\vec{F}_O=\vec{0}$

Por ser los dos de la misma masa, los momentos de los dos pesos se anulan mutuamente. El de la fuerza del soporte se anula por estar aplicado en el centro de reducción.

Por tanto, el momento cinético se conserva. Para que esto ocurra, el mono y los plátanos deben moverse con la misma velocidad. Veámoslo

$\vec{L}_O=\overrightarrow{OP}\times(m\vec{v}_P)+\overrightarrow{OM}\times(m\vec{v}_M)=(mRv_p)(+\vec{k})+(mRv_M)(-\vec{k})=mR(v_P-v_M)\vec{k}$

Como inicialmente esto valía 0, debe seguir siendo nulo. Por tanto

$v_P=v_M\,$

y los dos suben a la vez.

Test del segundo parcial 2017-2018 (GIE)

De Laplace

Contenido

1 Cuerpo en plano inclinado

2 Polea con hilos tensos

3 Fuerza central

4 Radio de curvatura

5 Sistema de partículas

5.1 Pregunta 1

5.2 Pregunta 2

6 Oscilador amortiguado

7 El mono y los plátanos

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES