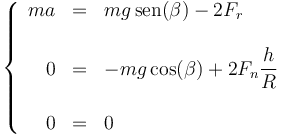Esfera que rueda por un carril
De Laplace
1 Enunciado
En los experimentos de Galileo, éste hizo rodar una esfera de radio R por un carril de anchura 2b (b < R), de forma que la bola rueda apoyada en los bordes del carril, minimizando el rozamiento.
El carril se encuentra inclinado un ángulo β respecto a la horizontal.
La bola posee masa m y un momento de inercia I = γmR2 (con \gamma entre 2/5, esfera maciza y 2/5, esfera hueca).
Suponiendo que las fuerzas a ambos lados del carril son simétricas, determine la aceleración con la que la bola desciende por el carril, si inicialmente se encuentra en reposo.
Determine el ángulo β máximo para el carril si no se desea que la bola deslice.
Supóngase ahora que existe un rozamiento por rodadura de forma que en los puntos de contacto se ejerce una fuerza adicional 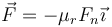 , siendo el eje X el tangente al carril en la dirección de avance. ¿Cuál es en ese caso la aceleración de la bola?
, siendo el eje X el tangente al carril en la dirección de avance. ¿Cuál es en ese caso la aceleración de la bola?
2 Solución
Tomaremos un sistema de ejes en el que OX es el eje tangente al plano inclinado, OY el normal a él en el plano de movimiento y OZ el ortogonal a ambos hacia afuera del plano.
La esfera se encuentra sometida a una serie de fuerzas:
- Su peso
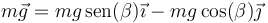
- Las fuerzas normales en los puntos de contacto A y B. Estas fuerzas son normales a la superficie de la esfera y por tanto son radiales.
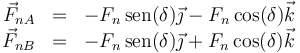
- por simetría, las dos reacciones tienen el mismo módulo y direcciones simétricas. \delta es el ángulo que el vector radial forma con la superficie del plano. Este águlo verifica
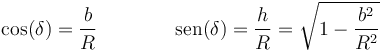
- Las fuerzas de tangenciales en los puntos de contacto. De nuevo por simetría, ambas son iguales. Estas fuerzas son de rozamiento estático, ya que la velocidad en los puntos de contacto es nula
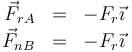
- para que no haya deslizamiento, estas fuerzas deben cumplir
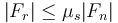
de manera que la aceleración del CM cumple la ecuación
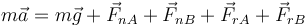
Separando en componentes