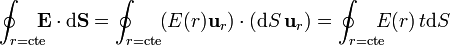Campo debido a una superficie esférica cargada

De Laplace

Revisión a fecha de 11:26 29 nov 2008; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución
- 2.1 Aplicando las leyes de la electrostática
- 2.2 Por integración directa

1 Enunciado

Una esfera de radio $R$ almacena una carga $Q$ distribuida uniformemente en su superficie. Calcule el campo eléctrico producido por la esfera en todos los puntos del espacio

Aplicando las leyes de la electrostática
Por integración directa

2 Solución

2.1 Aplicando las leyes de la electrostática

La forma más sencilla de calcular este campo es aplicando el caracter irrotacional del campo electrostático y la ley de Gauss.

El hecho de que el campo electrostático es irrotacional nos permite introducir el potencial eléctrico

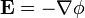
$\nabla\times\mathbf{E}=\mathbf{0}$ $\mathbf{E}=-\nabla\phi$

El uso del potencial eléctrico nos permite aprovechar de forma sencilla las simetrías de este problema.

Por tratarse de una superficie esférica uniformemente cargada, el sistema es invariante ante una rotación alrededor de su centro. Por ello, el potencial eléctrico no puede depender de las coordenadas esféricas $θ$ y $\varphi$

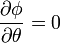
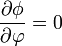
$\frac{\partial \phi}{\partial\theta} = 0$ $\frac{\partial \phi}{\partial\varphi} = 0$

Por tanto, el potencial eléctrico depende exclusivamente de la distancia al centro de la esfera

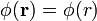
$\phi(\mathbf{r}) = \phi(r)$

y esto implica que el campo electrostático es un campo central

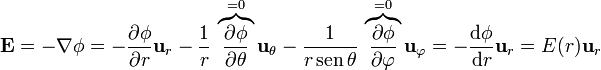
$\mathbf{E}=-\nabla\phi = - \frac{\partial \phi}{\partial r}\mathbf{u}_r - \frac{1}{r}\,\overbrace{\frac{\partial \phi}{\partial\theta}}^{=0}\mathbf{u}_\theta -\frac{1}{r\,\mathrm{sen}\,\theta}\,\overbrace{\frac{\partial \phi}{\partial\varphi}}^{=0}\mathbf{u}_\varphi = -\frac{\mathrm{d}\phi}{\mathrm{d}r}\mathbf{u}_r = E(r)\mathbf{u}_r$

Una vez establecido que el campo es radial y dependiente exclusivamente de la distancia al centro, podemos utilizar la ley de Gauss para hallar su valor.

Supongamos una superficie esférica de radio $r$ , concéntrica con la esfera de carga (pero de radio diferente, $r$ puede tener cualquier valor, mayor o menor que $R$ , el radio de la esfera cargada). De acuerdo con la ley de Gauss

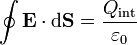
$\oint \mathbf{E}\cdot\mathrm{d}\mathbf{S}= \frac{Q_\mathrm{int}}{\varepsilon_0}$

Vamos primero con el primer miembro. Para una superficie esférica tenemos que

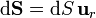
$\mathrm{d}\mathbf{S} = \mathrm{d}S\,\mathbf{u}_{r}$

por lo que el flujo se reduce a la integral

$\oint_{r=\mathrm{cte}} \!\!\!\!\mathbf{E}\cdot\mathrm{d}\mathbf{S} = \oint_{r=\mathrm{cte}} \!\!\left(E(r)\mathbf{u}_r\right)\cdot\left(\mathrm{d}S\,\mathbf{u}_r\right) = \oint_{r=\mathrm{cte}} \!\!\!\!E(r)\,t\mathrm{d}S$

2.2 Por integración directa

Campo debido a una superficie esférica cargada

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Aplicando las leyes de la electrostática

2.2 Por integración directa

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES