Dilatación y compresibilidad (GIE)
De Laplace
Contenido |
1 Introducción
Una de las propiedades termométricas de uso más frecuente es la dilatación o contracción de una columna de un líquido (mercurio o alcohol) o de una fina metálica.
Estos termómetros se basan en el hecho empírico de que la longitud de una porción de material cambia con la temperatura (normalmente expandiéndose al aumentar ésta). La causa microscópica de este fenómeno es la variación de la energía cinética de los átomos del material, lo que provoca un cambio en las distancias de equilibrio entre los diferentes átomos, y que se traduce en una dilatación (o contracción) macroscópica.
2 Coeficiente de dilatación lineal
Considerando solo variables macroscópicas, la longitud de una porción de material será una función de la temperatura
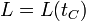
donde en general esta función podrá ser muy complicada.
Si consideramos pequeñas dilataciones de una pieza respecto a la longitud L0 que mide cuando la temperatura es t0, tenemos que en primera aproximación la dilatación de una pieza es proporcional a la propia longitud de la pieza, es decir, si una barra de 1 m se dilata 1 mm, una de 2 m s dilatará 2 mm. Por ello
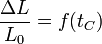
siendo f(tC) una cierta función de la temperatura, pero no de la longitud de la pieza. Esta función se anula en t0 y si nos separamos poco de esta temperatura podemos hacer una aproximación lineal y admitir que la dilatación es proporcional al incremento de temperatura (si con un incremento de 1°C se dilata 1 mm, con 2°C se dilata 2 mm), por lo que podemos escribir
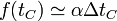
o, equivalentemente
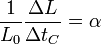
y

El factor α es el denominado coeficiente de dilatación lineal. Rigurosamente se define empleando derivadas en lugar de incrementos
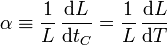
Las unidades en que se mide α en el SI son K − 1 (aunque, dado que se define a partir de incrementos, también pueden emplearse 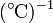 : normalmente es un valor muy pequeño, por lo que suelen usarse submúltiplos para expresarlo.
: normalmente es un valor muy pequeño, por lo que suelen usarse submúltiplos para expresarlo.
El coeficiente de dilatación lineal es una función de la temperatura, ya que se calcula a partir de la derivada en un cierto punto tC = t0. Si se halla a una temperatura diferente dará otro resultado (aunque si las temperaturas son próximas, los dos valores serán casi iguales).
Algunos valores de este coeficiente son
| Material | 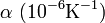 a 20°C | Material | 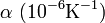 a 20°C | Material | 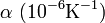 a 20°C | Material | 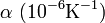 a 20°C |
|---|---|---|---|---|---|---|---|
| Aluminio | 23 | Agua | 69 | Acero inox. | 17.3 | Diamante | 1 |
| Etanol | 250 | Hierro | 11.8 | Hormigón | 12 | Mercurio | 61 |
| Oro | 14 | Plata | 18 | Vidrio | 8.5 | YbGaGe | ∼0 |
3 Coeficiente de dilatación superficial
El mismo principio se puede aplicar al área de una superficie sólida, que se dilata o contrae como consecuencia de la variación de la temperatura. Siguiendo el mismo razonamiento queda
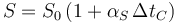
siendo αS el coeficiente de dilatación superficial, que se puede definir, para una temperatura fijada, como
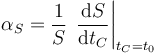
El coeficiente de dilatación superficial puede relacionarse con el dilatación lineal. Salvo en casos muy poco frecuentes, cuando una pieza de un material se dilata, todas sus dimensiones se multiplican en la misma proporción. Esto quiere decir que si tenemos una chapa metálica rectangular de base b0 y altura h0 a una temperatura t0, y la sometemos a un incremento de temperatura ΔtC, su nueva área será
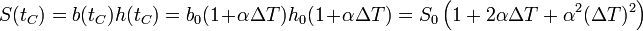
Puesto que las dilataciones son usualmente muy pequeñas el último término es despreciable, por lo que se puede hacer la aproximación
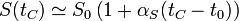
donde el coeficiente de dilatación superficial es igual al doble del lineal
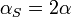
Hay que destacar que en una dilatación superficial (o volumétrica) todas las dimensiones se ven incrementadas. Esto quiere decir que si tenemos una pieza con un agujero, el tamaño del agujero aumenta con la temperatura, no se ve reducido porque el material rellene el agujero al dilatarse.
4 Coeficiente de dilatación volumétrico
De la misma manera que para una superficie, tenemos el aumento de volumen de un bloque como consecuencia del aumento de la temperatura
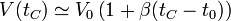
donde el coeficiente de dilatación volumétrico es aproximadamente igual al triple del lineal
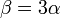
El coeficiente de dilatación volumétrico puede definirse sin necesidad de pasar por el lineal, como
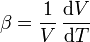
4.1 Variación en la densidad
Si un bloque de un material se dilata su densidad disminuye, ya que la masa del bloque permanece constante. La variación de la densidad la obtenemos imponiento la conservación de la masa
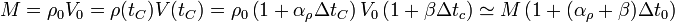
Puesto que la masa no varía con la temperatura, debe ser
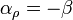
lo que nos da la disminución de la densidad
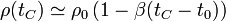
y una definición alternativa del coeficiente de dilatación volumétrico si lo que se conoce es la densidad como función de la temperatura:
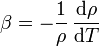
5 Caso de un gas ideal
En el caso de un gas ideal es sencillo calcular el coeficiente de dilatación volumétrico. Para una presión dada el volumen es proporcional a la temperatura según la ley de Charles
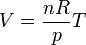
Derivando respecto a la temperatura y dividiendo por el propio volumen
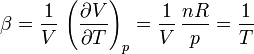
El símbolo de derivada parcial, y el subíndice p se incluyen para recordar que se trata de la derivada respecto a la temperatura, manteniendo constante la presión.
Para una temperatura de 25°C, este coeficiente de dilatación será igual
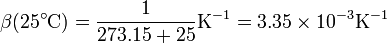
Esto quiere decir que si tenemos 1 l de gas a 25°C y subimos su temperatura 1°C (o 1 K) manteniendo constante su presión, el volumen aumenta en 3.35 cm³.
6 Anomalía térmica del agua
En la dilatación el agua posee propiedades que la hacen única. Si se mide experimentalmente la densidad del agua a diferentes temperaturas, se obtiene la tabla
| 
| 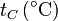
| 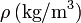
| 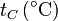
| 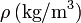
|
|---|---|---|---|---|---|
| 0 | 999.8395 | 20 | 998.2071 | 40 | 992.2 |
| 4 | 999.9720 | 22 | 997.7735 | 60 | 983.2 |
| 10 | 999.7026 | 25 | 997.0479 | 80 | 971.8 |
| 15 | 999.1026 | 30 | 995.6502 | 100 | 958.4 |
¿Qué tiene de especial esta tabla? Que primero aumenta y luego disminuye. Para temperaturas comprendidas entre 0°C y 4°C un incremento en la temperatura produce una contracción del agua. A 4°C, la densidad del agua alcanza un máximo y en este punto su derivada respecto a la temperatura, que nos da el coeficiente de dilatación volumétrico, se anula.