Inducción magnética FII GIA
De Laplace
Contenido |
1 Introducción
Hemos visto campos eléctricos estáticos creados por cargas eléctricas en reposo, y campos magnéticos estáticos creados por corrientes estacionarias. Hasta ahora los fenómenos eléctricos y magnéticos han estado desacoplados. Esto quiere decir que no hemos visto fenómenos en que un campo eléctrico interfiera con un magnético y viceversa.
Esto cambia cuando se consideran situaciones en que los campos cambian en el tiempo. Estudiaremos primero el fenómeno de la inducción magnética, en el que un campo magnético variable en el tiempo genera un campo eléctrico.
Este fenómeno fue descubierto en 1831 independientemente por Michael Faraday(1791-1867) en Inglaterra y Joseph Henry(1797-1878) en Estados Unidos.
Faraday y Henry descubrieron que un campo magnético variable en el tiempo puede generar una corriente eléctrica en un conductor. Esto significa que un campo magnético variable genera un campo eléctrico. Este campo eléctrico no es electrostático, es decir, no está generado por cargas eléctricas. Como consecuencia, no es conservativo.
El fenómeno de inducción magnética tiene innumerables aplicaciones tecnológicas. Casi toda la generación de electricidad usa este efecto. Los motores eléctricos y los transformadores funcionan basándose en este fenómeno.
2 Flujo magnético
Dada una superficie en el seno de un campo magnético, el flujo magnético es proporcional al número de líneas de campo magnético que atraviesan esa superficie. Se calcula de manera similar al flujo del campo eléctrico
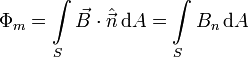
La unidad de flujo magnético es el Weber
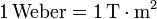
2.1 Espira en un campo magnético uniforme
Si tenemos una espira plana, de modo que el vector normal a ella forma un ángulo θ con el campo magnético uniforme, el flujo a través de la espira es
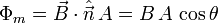
Si en vez de una espira es una bobina con N vueltas, el flujo total es el flujo a través de una vuelta de la bobina multiplicado por el número de vueltas
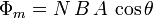
3 Fem inducida: Ley de Faraday
Los experimentos muestran que si una espira conductora se encuentra en el seno de un campo magnético que cambia con el tiempo, aparece una corriente en la espira.
Se dice que el campo magnético variable produce una fem inducida.
La ley que da el valor de la fem inducida es la regla del flujo
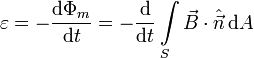
Φm es el flujo del campo magnético que atraviesa una superficie apoyada en la espira. Si la espira es una circunferencia, esta superficie podría ser el círculo definido por la espira.
El sentido negativo se refiere al sentido de la corriente que aparece. Veremos más tarde este sentido al hablar de la Ley de Lenz.
Otra forma de entender esta ley es que la fem inducida se produce al cambiar el número de líneas de campo que atraviesa la superficie definida por la espira. Así es como la formuló Faraday.
El flujo magnético puede variar por diferentes causas:
- Si el campo magnético es producido por una corriente, cambia al variar la intensidad de ésta.
- Si el campo magnético es producido por un imán, cambia en el tiempo si el imán se desplaza respecto a la espira.
- Si el campo magnético no cambia en el tiempo, el flujo puede cambiar porque la espira se mueva, rote o se deforme.
La corriente en la espira implica que debe haber una fuerza que ponga las cargas en movimiento. Esta fuerza no puede ser magnética, pues las cargas en principio están en reposo. Además el campo magnético no puede realizar trabajo sobre las cargas, y la fem empuja las cargas en el circuito compensando la energía perdida por efecto Joule. Las cargas se mueven debido a que aparece un campo eléctrico inducido,  . Este campo empuja las cargas a lo largo de la espira. La fem inducida es el trabajo por unidad de carga realizado por este campo en toda la espira
. Este campo empuja las cargas a lo largo de la espira. La fem inducida es el trabajo por unidad de carga realizado por este campo en toda la espira
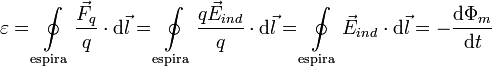
Este campo eléctrico es no conservativo, pues su circulación en un contorno cerrado es no nula. Para producir una corriente que se mantenga en el tiempo el campo no puede ser conservativo.
De hecho, este campo aparece aunque no esté la espira. Podemos imaginar la curva Γque define la espira, pero sin que esté ella. Si en esa región hay un campo magnético variable, aparece un campo eléctrico de modo que se cumple
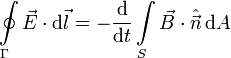
La superficie S es una superficie cualquiera que se apoye en el contorno Γ.





