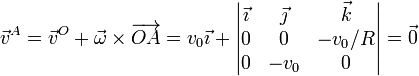Entrar Página Discusión Historial Go to the site toolbox

4.8. Rodadura permanente de un disco

De Laplace

1 Enunciado

La rodadura permanente de un disco de radio R sobre una superficie horizontal puede describirse mediante el campo de velocidades

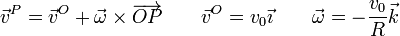
\vec{v}^P = \vec{v}^O +\vec{\omega}\times\overrightarrow{OP}\qquad\vec{v}^O = v_0\vec{\imath}\qquad\vec{\omega}=-\frac{v_0}{R}\vec{k}

donde la superficie horizontal se encuentra en y = − R.

  1. Determine, para un instante dado, la velocidades de los puntos A, B, C y D situados en los cuatro cuadrantes del disco.
  2. Calcule la aceleración de estos puntos para el mismo instante, suponiendo v0 = cte.

2 Velocidades

Para cada uno de los puntos, basta aplicar la fórmula correspondiente

Punto A
Su vector de posición relativa es
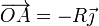
\overrightarrow{OA}=-R\vec{\jmath}
por lo que su velocidad vale
\vec{v}^A = \vec{v}^O +\vec{\omega}\times\overrightarrow{OA}=v_0\vec{\imath}+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 0 & 0 & -v_0/R \\ 0 & -v_0 & 0 \end{matrix}\right| = \vec{0}

3 Aceleraciones

Obtenido de "http://tesla.us.es/wiki/index.php/4.8._Rodadura_permanente_de_un_disco"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace