Espira cuadrada en campo no uniforme
De Laplace
Contenido |
1 Enunciado
En una región del espacio existe un campo magnético

Una espira cuadrada de lado a y resistencia R se encuentra situada en el plano z = 0 con sus lados paralelos a los ejes. La espira se mueve de forma que su extremo trasero se encuentra en la posición x = v0t.
- Calcule la corriente que circula por la espira.
- Halle la fuerza que el campo magnético ejerce sobre la espira.
- Calcule la potencia disipada en la espira y la energía total disipada durante un tiempo T.
2 Corriente inducida
La corriente que circula por la espira se calcula por aplicación de la ley de Faraday
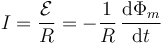
Calculamos el flujo magnético a través de un cuadrado apoyado en la espira. Asignamos un sentido de recorrido antihorario para la corriente, de forma que la normal a la superficie sobre la que calculamos el flujo va en la dirección de  .
.
El campo magnético en todos los puntos de esta superficie vale
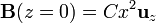
En este caso
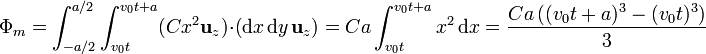
Derivando respecto al tiempo
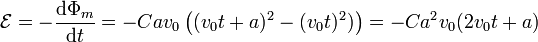
y finalmente la corriente es
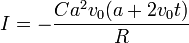
Esta corriente varía linealmente en el tiempo. Es nula en el instante t0 = − (a / 2) / v0, para el cual la espira está centrada en el campo. Es positiva para t < t0, en que el flujo magnético está disminuyendo y la corriente inducida tiende a aumentarlo. Es positiva para t > t0, en el que el flujo magnético está aumentando y la corriente intenta disminuirlo.





