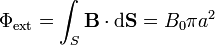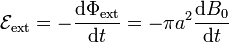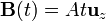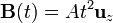Espira circular en un campo variable
De Laplace
Contenido |
1 Enunciado
Una espira circular de radio 
, con autoinducción 
y resistencia 
, se encuentra sometida a un campo magnético uniforme en el espacio pero variable en el tiempo. El campo es perpendicular al plano de la espira.
Calcule la corriente que circula por la espira si el campo magnético varía en el tiempo, durante un largo intervalo, como
2 Solución
2.1 Planteamiento general
En todos los casos por la espira circula una corriente debida a la presencia de una fuerza electromotriz causada por el cambio en el flujo magnético
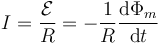
Este flujo magnético es la superposición de dos contribuciones: la debida al campo externo y la debida a la propia espira. Ésta última es proporcional a la corriente que circula por la espira
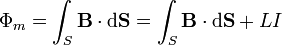
lo que da la ecuación diferencial
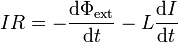
o, reordenando términos
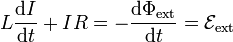
En términos del circuito equivalente, este sencillo sistema equivale a tres elementos de circuito: una resistencia R, una autoinducción L y un generador de f.e.m.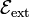 
.
En todos los casos de este problema, el campo magnético externo es uniforme, aunque dependiente del tiempo. Por ello, el flujo magnético y la fuerza electromotriz externa valen
