Entrar Página Discusión Historial Go to the site toolbox

Densidades de carga de polarización

De Laplace

(Diferencias entre revisiones)
m (→Demostración)
(→Demostración)
Línea 46: Línea 46:
Aplicando que <math>\mathrm{d}\mathbf{S}'=\mathbf{n}'\cdot\mathrm{d}S'</math> obtenemos finalmente la expresión deseada
Aplicando que <math>\mathrm{d}\mathbf{S}'=\mathbf{n}'\cdot\mathrm{d}S'</math> obtenemos finalmente la expresión deseada
-
<center><math>\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\left(\oint_{\partial\tau}\frac{\sigma_p(\mathbf{r}')\,\mathrm{d}S'}{|\mathbf{r}-\mathbf{r}'|}\right)\,\mathrm{d}\tau'-\int_\tau \frac{\rho_p(\mathbf{r}')}{|\mathbf{r}-\mathbf{r'}'}\mathrm{d}\tau'</math></center>
+
<center><math>\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\oint_{\partial\tau}\frac{\sigma_p(\mathbf{r}')\,\mathrm{d}S'}{|\mathbf{r}-\mathbf{r}'|}\right)\,\mathrm{d}\tau'+\frac{1}{4\pi\varepsilon_0}\int_\tau \frac{\rho_p(\mathbf{r}')}{|\mathbf{r}-\mathbf{r'}'}\mathrm{d}\tau'</math></center>
==Densidad de carga libre==
==Densidad de carga libre==

Revisión de 20:37 30 ene 2010

Contenido

1 Introducción

2 Potencial debido a una polarización

3 Densidades de carga de polarización

La expresión del potencial debido a un volumen polarizado puede transformarse en suma de dos integrales

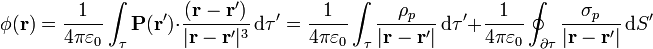
\phi(\mathbf{r}) =\frac{1}{4\pi\varepsilon_0}\int_\tau \mathbf{P}(\mathbf{r}'){\cdot}\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}\tau' = \frac{1}{4\pi\varepsilon_0}\int_\tau\frac{\rho_p}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}\tau'+ \frac{1}{4\pi\varepsilon_0}\oint_{\partial\tau}\frac{\sigma_p}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}S'

donde

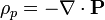\rho_p=-\nabla\cdot\mathbf{P}    y    \sigma_p=\mathbf{n}\cdot\mathbf{P}

son las llamadas densidades de carga de polarización. Aquí \mathbf{n} es la normal exterior a la superficie del material polarizado.

La ventaja de esta transformación en suma de dos integrales es que este tipo de integrales corresponden al potencial debido a distribuciones de carga eléctrica. De esta forma se reduce un problema nuevo (el potencial debido a una distribución continua de dipolos) a uno ya conocido (el potencial de distribuciones de cargas)

En términos físicos, esto equivale a decir que una polarización es equivalente a una superposición de dos distribuciones de carga, una volumétrica y otra superficial.

3.1 Volumétrica

3.2 Superficial

3.3 Demostración

Para demostrar la equivalencia entre ambas expresiones, simplemente usamos la relación vectorial

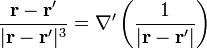
\frac{\mathbf{r}-\mathbf{r}'}{|\mathbf{r}-\mathbf{r}'|^3} = \nabla'\left(\frac{1}{|\mathbf{r}-\mathbf{r}'|}\right)

donde la prima sobre el operador nabla significa que las derivadas son respecto a las coordenadas con prima (las posiciones de las fuentes).

De esta forma el potencial debido a la polarización se puede escribir

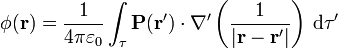
\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\int_\tau\mathbf{P}(\mathbf{r'})\cdot\nabla'\left(\frac{1}{|\mathbf{r}-\mathbf{r}'|}\right)\,\mathrm{d}\tau'

Usando ahora el álgebra del operador nabla

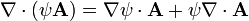
\nabla\cdot(\psi\mathbf{A}) = \nabla\psi\cdot\mathbf{A}+\psi\nabla\cdot\mathbf{A}

podemos transformar la integral en

\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\left(\int_\tau\nabla'\cdot\left(\frac{\mathbf{P}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\right)\,\mathrm{d}\tau'-\int_\tau \frac{\nabla'\cdot\mathbf{P}}{|\mathbf{r}-\mathbf{r'}'}\mathrm{d}\tau'\right)

Aplicando el teorema de Gauss a la primera integral la transformamos en una de superficie

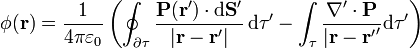
\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\left(\oint_{\partial\tau}\frac{\mathbf{P}(\mathbf{r}')\cdot\mathrm{d}\mathbf{S}'}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}\tau'-\int_\tau \frac{\nabla'\cdot\mathbf{P}}{|\mathbf{r}-\mathbf{r'}'}\mathrm{d}\tau'\right)

Aplicando que 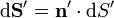\mathrm{d}\mathbf{S}'=\mathbf{n}'\cdot\mathrm{d}S' obtenemos finalmente la expresión deseada

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\oint_{\partial\tau}\frac{\sigma_p(\mathbf{r}')\,\mathrm{d}S'}{|\mathbf{r}-\mathbf{r}'|}\right)\,\mathrm{d}\tau'+\frac{1}{4\pi\varepsilon_0}\int_\tau \frac{\rho_p(\mathbf{r}')}{|\mathbf{r}-\mathbf{r'}'}\mathrm{d}\tau'

4 Densidad de carga libre

5 Carga y momento de ρp y σp

Como a toda densidad de carga, a la de polarización se le puede calcular sus momentos multipolares, con el fin de aproximar el potencial que produce una distribución de dipolos en puntos alejados de ella.

5.1 Carga neta

La carga neta (momento monopolar) de una distribución de carga de polarización es siempre nula

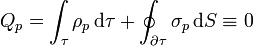
Q_p=\int_\tau \rho_p\,\mathrm{d}\tau+\oint_{\partial\tau}\sigma_p\,\mathrm{d}S\equiv 0

Este resultado es una consecuencia de que la distribución de carga de polarización es equivalente a un conjunto de dipolos. Puesto que cada dipolo es eléctricamente neutro, la carga total del sistema es nula.

Podemos demostrar este resultado a partir de las definiciones de ρp y σp, por aplicación del teorema de Gauss. Por un lado tenemos que

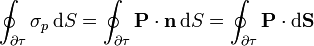
\oint_{\partial\tau}\sigma_p\,\mathrm{d}S=\oint_{\partial\tau}\mathbf{P}\cdot\mathbf{n}\,\mathrm{d}S=\oint_{\partial\tau}\mathbf{P}\cdot\mathrm{d}\mathbf{S}

y por otro

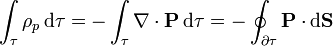
\int_{\tau}\rho_p\,\mathrm{d}\tau=-\int_{\tau}\nabla\cdot\mathbf{P}\,\mathrm{d}\tau=-\oint_{\partial\tau}\mathbf{P}\cdot\mathrm{d}\mathbf{S}

Sumando los dos términos

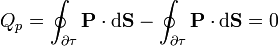
Q_p = \oint_{\partial\tau}\mathbf{P}\cdot\mathrm{d}\mathbf{S}-\oint_{\partial\tau}\mathbf{P}\cdot\mathrm{d}\mathbf{S} = 0

5.2 Momento dipolar

El momento dipolar de la distribución de cargas de polarización equivale a la integral de la polarización

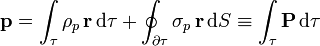
\mathbf{p}= \int_\tau \rho_p\,\mathbf{r}\,\mathrm{d}\tau+\oint_{\partial\tau}\sigma_p\,\mathbf{r}\,\mathrm{d}S \equiv\int_\tau\mathbf{P}\,\mathrm{d}\tau

De nuevo este resultado es elemental: si la polarización es la densidad de momento dipolar, su integral nos dará el momento dipolar total.

La demostración es similar a la anterior pero, al tratarse de vectores, es un poco más complicada. Puede hacerse considerando por separado cada una de las componentes cartesianas del momento dipolar.

6 Ecuaciones de la electrostática en dieléctricos

Obtenido de "http://tesla.us.es/wiki/index.php/Densidades_de_carga_de_polarizaci%C3%B3n"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace