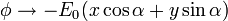Partícula elíptica en campo eléctrico oblicuo
De Laplace
(Diferencias entre revisiones)
(→Planteamiento) |
(→Planteamiento) |
||
| Línea 4: | Línea 4: | ||
El problema del potencial se convierte en la solución de la ecuación de Laplace | El problema del potencial se convierte en la solución de la ecuación de Laplace | ||
| - | <math>\nabla^2\phi = 0</math> | + | <center><math><math>\nabla^2\phi = 0</math></math></center> |
| + | |||
| + | con la condición de Neumann en la superficie de la partícula | ||
<center><math>\mathbf{n}\cdot\nabla\phi = 0\qquad(\mathbf{r}\in S)</math></center> | <center><math>\mathbf{n}\cdot\nabla\phi = 0\qquad(\mathbf{r}\in S)</math></center> | ||
Revisión de 18:38 12 ene 2010
Contenido |
1 Planteamiento
Tenemos una elipse de semiejes a y b (a > b) recubierta de una capa doble. La partícula está sometida a un campo eléctrico que en el infinito es uniforme y forma un ángulo α con el semieje mayor.
El problema del potencial se convierte en la solución de la ecuación de Laplace
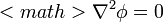</math>con la condición de Neumann en la superficie de la partícula
y con el comportamiento asintótico
