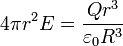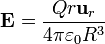Campo debido a una esfera cargada uniformemente

De Laplace

(Diferencias entre revisiones)

Revisión de 17:25 9 ene 2010

1 Enunciado

Una esfera de radio $R$ almacena una carga $Q$ distribuida uniformemente en su volumen.

Calcule el campo eléctrico producido por la esfera en todos los puntos del espacio.
Halle la fuerza que experimenta un dipolo $\mathbf{p}$ situado en el interior de esta nube de carga.

2 Campo eléctrico

El campo eléctrico se determina de forma simple mediante la aplicación de la ley de Gauss.

Dada la simetría del sistema, podemos suponer que el potencial eléctrico debido a esta esfera depende exclusivamente de la distancia al centro de ella. Esto implica que el campo eléctrico debido a la esfera es central

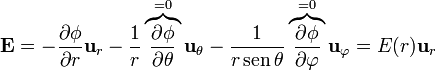
$\phi=\phi(r)\,$ $\Rightarrow$ $\mathbf{E}=-\frac{\partial\phi}{\partial r}\mathbf{u}_r-\frac{1}{r}\overbrace{\frac{\partial\phi}{\partial\theta}}^{=0}\mathbf{u}_\theta-\frac{1}{r\,\mathrm{sen}\,\theta}\overbrace{\frac{\partial\phi}{\partial\varphi}}^{=0}\mathbf{u}_\varphi=E(r)\mathbf{u}_r$

Si calculamos el flujo del campo eléctrico a través de una superficie esférica de radio $r$ concéntrica con la esfera de carga obtenemos

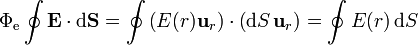
$\Phi_\mathrm{e}\oint \mathbf{E}\cdot\mathrm{d}\mathbf{S}=\oint \left(E(r)\mathbf{u}_r\right)\cdot\left(\mathrm{d}S\,\mathbf{u}_r\right)=\oint E(r)\,\mathrm{d}S$

Al tratarse de dos vectores paralelos, el integrando se reduce al producto de las dos componentes radiales. Por otro lado, por ser la superficie de integración una esfera ( $r = cte$ ) y ser el campo central la componente radial del campo es la misma sobre todos los puntos de la superficie y puede extraerse de la integral

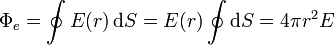
$\Phi_e = \oint E(r)\,\mathrm{d}S= E(r)\oint \mathrm{d}S =4\pi r^2 E$

Nótese que lo que es constante es la componente radial del campo y no el propio campo, cuya dirección varía de un punto a otro de la superficie esférica.

Este resultado es general para cualquier sistema con simetría esférica, sea una carga puntual, una superficie cargada o una distribución radial no uniforme.

De acuerdo con la ley de Gauss, este flujo es igual a la carga encerrada, dividida por la permitividad del vacío

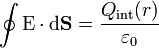
$\oint \mathrm{E}\cdot\mathrm{d}\mathbf{S}=\frac{Q_\mathrm{int}(r)}{\varepsilon_0}$

Dependiendo de si el radio de la superficie de integración es mayor o menor que el de la esfera de carga, tenemos dos casos:

En el exterior de la nube de carga ( $r > R$ ): En este caso, la superficie de integración contiene a toda la carga del sistema

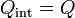
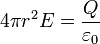
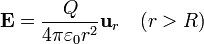
$Q_\mathrm{int}=Q\,$ $\Rightarrow$ $4\pi r^2 E = \frac{Q}{\varepsilon_0}$ $\Rightarrow$ $\mathbf{E}=\frac{Q}{4\pi\varepsilon_0r^2}\mathbf{u}_r\quad(r>R)$

El campo en el exterior de la esfera es igual al de una carga puntual que concentrara toda la carga del sistema y estuviera situada en el centro de ésta.

En el interior de la nube ( $r < R$ ): En este caso la superficie de integración no contiene a toda la carga del sistema, sino solo a la porción que quepa dentro de ella. Puesto que la densidad de carga es uniforme, esta carga encerrada es igual a la densidad de carga multiplicada por el volumen de esta esfera:

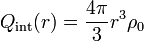
$Q_\mathrm{int}(r) = \frac{4\pi}{3}r^3\rho_0$

A su vez, la densidad de carga es igual a la carga total dividida por el volumen total

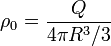
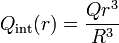
$\rho_0 = \frac{Q}{4\pi R^3/3}$ $\Rightarrow$ $Q_\mathrm{int}(r)=\frac{Qr^3}{R^3}$

lo que nos da el campo eléctrico

$4\pi r^2 E = \frac{Qr^3}{\varepsilon_0R^3}$ $\Rightarrow$ $\mathbf{E}=\frac{Qr\mathbf{u}_r}{4\pi\varepsilon_0R^3}$

3 Fuerza sobre un dipolo

@@ Línea 33: / Línea 33: @@
 <center><math>Q_\mathrm{int}=Q\,</math>{{tose}}<math>4\pi r^2 E = \frac{Q}{\varepsilon_0}</math> {{tose}}<math>\mathbf{E}=\frac{Q}{4\pi\varepsilon_0r^2}\mathbf{u}_r\quad(r>R)</math></center>
+:El campo en el exterior de la esfera es igual al de una carga puntual que concentrara toda la carga del sistema y estuviera situada en el centro de ésta.
+;En el interior de la nube (<math>r<R</math>): En este caso la superficie de integración no contiene a toda la carga del sistema, sino solo a la porción que quepa dentro de ella. Puesto que la densidad de carga es uniforme, esta carga encerrada es igual a la densidad de carga multiplicada por el volumen de esta esfera:
+<center><math>Q_\mathrm{int}(r) = \frac{4\pi}{3}r^3\rho_0</math></center>
+A su vez, la densidad de carga es igual a la carga total dividida por el volumen total
+<center><math>\rho_0 = \frac{Q}{4\pi R^3/3}</math>{{tose}}<math>Q_\mathrm{int}(r)=\frac{Qr^3}{R^3}</math></center>
+lo que nos da el campo eléctrico
+<center><math>4\pi r^2 E = \frac{Qr^3}{\varepsilon_0R^3}</math>{{tose}}<math>\mathbf{E}=\frac{Qr\mathbf{u}_r}{4\pi\varepsilon_0R^3}</math></center>
 ==Fuerza sobre un dipolo==
 [[Categoría:Problemas de electrostática en el vacío]]

Campo debido a una esfera cargada uniformemente

De Laplace

Revisión de 17:25 9 ene 2010

1 Enunciado

2 Campo eléctrico

3 Fuerza sobre un dipolo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES