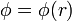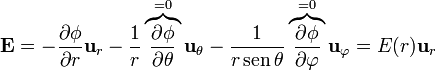Campo debido a una esfera cargada uniformemente
De Laplace
(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Nueva página: ==Enunciado== Una esfera de radio <math>R</math> almacena una carga <math>Q</math> distribuida uniformemente en su volumen. # Calcule el campo eléctrico producido por la esfera en t...)
Edición más nueva →
(Nueva página: ==Enunciado== Una esfera de radio <math>R</math> almacena una carga <math>Q</math> distribuida uniformemente en su volumen. # Calcule el campo eléctrico producido por la esfera en t...)
Edición más nueva →
Revisión de 16:45 9 ene 2010
1 Enunciado
Una esfera de radio R almacena una carga Q distribuida uniformemente en su volumen.
- Calcule el campo eléctrico producido por la esfera en todos los puntos del espacio.
- Halle la fuerza que experimenta un dipolo
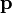situado en el interior de esta nube de carga.
2 Campo eléctrico
El campo eléctrico se determina de forma simple mediante la aplicación de la ley de Gauss.
Dada la simetría del sistema, podemos suponer que el potencial eléctrico debido a esta esfera depende exclusivamente de la distancia al centro de ella. Esto implica que el campo eléctrico debido a la esfera es central
