Entrar Página Discusión Historial Go to the site toolbox

Campo de un anillo no uniforme

De Laplace

(Diferencias entre revisiones)
(→Campo en el eje)
Línea 37: Línea 37:
<center><math>\mathbf{u}_{\rho'}=\cos\varphi'\,\mathbf{u}_x+\,\mathrm{sen}\,\varphi'\mathbf{u}_y</math></center>
<center><math>\mathbf{u}_{\rho'}=\cos\varphi'\,\mathbf{u}_x+\,\mathrm{sen}\,\varphi'\mathbf{u}_y</math></center>
 +
 +
lo que nos deja la integral como
 +
 +
<center><math>\mathbf{E}(z)=\frac{1}{4\pi\varepsilon_0}\int_{-\pi}^\pi \frac{\lambda_0\cos\varphi'(-R\cos\varphi'\mathbf{u}_x-R\,\mathrm{sen}\,\varphi'\mathbf{u}_y+z\mathbf{u}_z)\,R\,\mathrm{d}\varphi'}{(R^2+z^2)^{3/2}} </math></center>
 +
La primera tentación, al saber que el potencial es nulo en todos los puntos del eje es decir que el campo eléctrico, que es su gradiente, también lo es. Sin embargo, esto es incorrecto.
La primera tentación, al saber que el potencial es nulo en todos los puntos del eje es decir que el campo eléctrico, que es su gradiente, también lo es. Sin embargo, esto es incorrecto.

Revisión de 23:07 8 ene 2010

Contenido

1 Enunciado

En el plano XY se encuentra una distribución de carga lineal, formando un anillo, de radio R y con una distribución de carga no uniforme dada, en coordenadas cilíndricas, por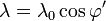
\lambda=\lambda_0\cos\varphi'    \varphi'\in(-\pi,\pi]
  1. Halle el potencial eléctrico producido por el anillo en los puntos del eje Z.
  2. Calcule el campo eléctrico producido por el anillo en el mismo eje.
  3. Demuestre que, para puntos alejados, su campo se comporta como el de un dipolo, ¿cuál sería el valor y la orientación de dicho dipolo?

2 Potencial en el eje

El potencial en el eje del anillo puede hallarse por integración directa, según la expresión

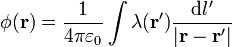
\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \lambda(\mathbf{r}')\frac{\mathrm{d}l'}{|\mathbf{r}-\mathbf{r}'|}

Tenemos que

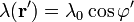
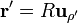
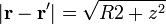
\lambda(\mathbf{r}')=\lambda_0\cos\varphi'        \mathbf{r}=z\mathbf{u}_z\,        \mathbf{r}'=R\mathbf{u}_{\rho'}\,        \mathbf{r}-\mathbf{r}'=-R\mathbf{u}_{\rho'}+z\mathbf{u}_z\,        |\mathbf{r}-\mathbf{r}'|=\sqrt{R2+z^2}        \mathrm{d}l'=|\mathrm{d}\mathbf{r}'|=R\,\mathrm{d}\varphi'

Sustituyendo todo esto queda la integral

\phi(z)=\frac{1}{4\pi\varepsilon_0}\int_{-\pi}^\pi \frac{\lambda_0\cos\varphi'\,R\,\mathrm{d}\varphi'}{\sqrt{R^2+z^2}} = \frac{\lambda_0 R}{4\pi\varepsilon_0\sqrt{R^2+z^2}}\int_{-\pi}^\pi \cos\varphi'\,\mathrm{d}\varphi'=0

Obtenemos entonces que el potencial es nulo en todos los puntos del eje.

Puede entenderse este resultado observando que, cuando se tienen dos cargas iguales y opuestas, el potencial es nulo en los puntos que equidistan de ambas. En este anillo, cuya densidad de carga es positiva en un lado y negativa en el otro, los puntos diametralmente opuestos poseen cargas de la misma magnitud y signo contrario. Por ello, en el eje, que equidista de dos puntos diametralmente opuestos, las contribuciones al potencial se anulan dos a dos y queda un potencial total nulo.

3 Campo en el eje

Calculamos el campo en los puntos del eje también por integración directa, según la ley,

\mathbf{E}(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \lambda(\mathbf{r}')\frac{(\mathbf{r}-\mathbf{r}')\mathrm{d}l'}{|\mathbf{r}-\mathbf{r}'|^3}

Sustituyendo cada factor, calculado anteriormente, nos queda la integral vectorial

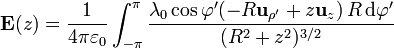
\mathbf{E}(z)=\frac{1}{4\pi\varepsilon_0}\int_{-\pi}^\pi \frac{\lambda_0\cos\varphi'(-R\mathbf{u}_{\rho'}+z\mathbf{u}_z)\,R\,\mathrm{d}\varphi'}{(R^2+z^2)^{3/2}}

A la hora de calcular esta integral vectorial hay que tener mucho cuidado con los vectores de la base que se empleen. Cuando se usa una base no cartesiana (la de cilíndricas, en este caso), esta base depende de la posición y por tanto debe tenerse en cuenta a la hora de integrar. Por ello, es casi siempre preferible el pasar a la base cartesiana, que posee la ventaja de que es independiente de la posición. En este caso

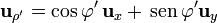
\mathbf{u}_{\rho'}=\cos\varphi'\,\mathbf{u}_x+\,\mathrm{sen}\,\varphi'\mathbf{u}_y

lo que nos deja la integral como

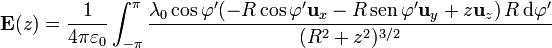
\mathbf{E}(z)=\frac{1}{4\pi\varepsilon_0}\int_{-\pi}^\pi \frac{\lambda_0\cos\varphi'(-R\cos\varphi'\mathbf{u}_x-R\,\mathrm{sen}\,\varphi'\mathbf{u}_y+z\mathbf{u}_z)\,R\,\mathrm{d}\varphi'}{(R^2+z^2)^{3/2}}


La primera tentación, al saber que el potencial es nulo en todos los puntos del eje es decir que el campo eléctrico, que es su gradiente, también lo es. Sin embargo, esto es incorrecto.

Podemos verlo físicamente de una forma sencilla

4 Desarrollo multipolar

Obtenido de "http://tesla.us.es/wiki/index.php/Campo_de_un_anillo_no_uniforme"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace