Ecuación de Van der Waals
De Laplace
(→Valores numéricos) |
|||
| Línea 29: | Línea 29: | ||
Sustituyendo los valores del enunciado tenemos, para la ecuación de estado de Van der Waals | Sustituyendo los valores del enunciado tenemos, para la ecuación de estado de Van der Waals | ||
| + | <center><math> | ||
| + | W_\mathrm{VdW}=-(1\,\mathrm{mol})\left(0.082\,\frac{\mathrm{atm}\cdot\mathrm{l}}{\mathrm{K}\cdot\mathrm{mol}}\right)(300\,\mathrm{K})\ln\left(\frac{3-0.122}{2-0.122}\right)+14.5\,\mathrm{atm}\cdot\mathrm{l}^2\left(\frac{1}{3\,\mathrm{l}}-\frac{1}{2\,\mathrm{l}}\right)=0-8.085\,\mathrm{atm}\cdot\mathrm{l}=-820\,\mathrm{J}</math></center> | ||
| + | |||
| + | Siguiendo el convenio habitual, este es el trabajo realizado ''sobre'' el gas. Si queremos el trabajo realizado ''por'' el gas, deberemos cambiarle el signo, quedando +820 J, que es positivo, como corresponde a una expansión contra una presión exterior. | ||
[[Categoría:Problemas del gas ideal]] | [[Categoría:Problemas del gas ideal]] | ||
Revisión de 10:22 28 abr 2009
Contenido |
1 Enunciado
El comportamiento del gas butano se ajusta, dentro de ciertos límites, a la ecuación de estado de Van der Waals

siendo en este caso a = 14.5 atm·l² y b = 0.122 l. Calcule el trabajo realizado por un mol de gas butano, considerándolo como un gas de Van der Waals, al expansionarse cuasiestáticamente desde 2 l hasta 3 l a la temperatura constante de t = 27°C. Compare con el resultado que daría la ecuación de los gases ideales.
2 Trabajo
Por tratarse de un proceso cuasiestático, podemos calcular el trabajo realizado sobre el gas mediante la integral
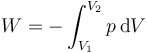
Despejando la presión de la ecuación de Van der Waals
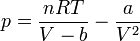
y sustituyendo e integrando
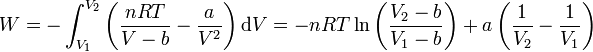
3 Comparación con el gas ideal
La ecuación de Van der Waals se reduce a la de los gases ideales cuando 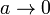 y
y 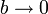 . Este límite lo podemos tomar directamente en la expresión del trabajo y nos queda
. Este límite lo podemos tomar directamente en la expresión del trabajo y nos queda

4 Valores numéricos
Sustituyendo los valores del enunciado tenemos, para la ecuación de estado de Van der Waals
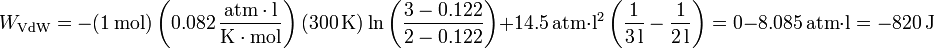
Siguiendo el convenio habitual, este es el trabajo realizado sobre el gas. Si queremos el trabajo realizado por el gas, deberemos cambiarle el signo, quedando +820 J, que es positivo, como corresponde a una expansión contra una presión exterior.





