Ecuación de Van der Waals
De Laplace
(→Trabajo) |
(→Comparación con el gas ideal) |
||
| Línea 22: | Línea 22: | ||
==Comparación con el gas ideal== | ==Comparación con el gas ideal== | ||
| + | La ecuación de Van der Waals se reduce a la de los gases ideales cuando <math>a\to 0</math> y <math>b\to 0</math>. Este límite lo podemos tomar directamente en la expresión del trabajo y nos queda | ||
| + | |||
| + | <center><math>W_\mathrm{ideal} = -nRT\ln\left(\frac{V_2}{V_1}\right)</math></center> | ||
==Valores numéricos== | ==Valores numéricos== | ||
[[Categoría:Problemas del gas ideal]] | [[Categoría:Problemas del gas ideal]] | ||
Revisión de 10:10 28 abr 2009
Contenido |
1 Enunciado
El comportamiento del gas butano se ajusta, dentro de ciertos límites, a la ecuación de estado de Van der Waals
siendo en este caso a = 14.5 atm·l² y b = 0.122 l. Calcule el trabajo realizado por un mol de gas butano, considerándolo como un gas de Van der Waals, al expansionarse cuasiestáticamente desde 2 l hasta 3 l a la temperatura constante de t = 27°C. Compare con el resultado que daría la ecuación de los gases ideales.
2 Trabajo
Por tratarse de un proceso cuasiestático, podemos calcular el trabajo realizado sobre el gas mediante la integral
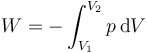
Despejando la presión de la ecuación de Van der Waals
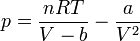
y sustituyendo e integrando
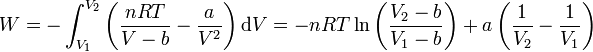
3 Comparación con el gas ideal
La ecuación de Van der Waals se reduce a la de los gases ideales cuando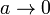 
y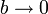 
. Este límite lo podemos tomar directamente en la expresión del trabajo y nos queda
