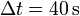Crecimiento de una capa de hielo
De Laplace
(Nueva página: == Enunciado == Un estanque de agua a <math>0\mathrm{^oC}</math> está cubierto por una capa de hielo de 4.00 cm de espesor. Si la temperatura del aire permanece constante a -10.0<ma...)
Edición más nueva →
Revisión de 11:41 16 abr 2009
1 Enunciado
Un estanque de agua a 0oC está cubierto por una capa de hielo de 4.00 cm de espesor. Si la temperatura del aire permanece constante a -10.0oC, ¿cuánto tardará el espesor de la capa de hielo en alcanzar los 8.00 cm?
2 Solución
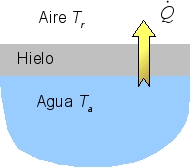
Intentemos primero comprender la física del problema. Como se indica en la figura, tenemos dos sistemas que intercambian calor, el agua líquida debajo del hielo y el aire por encima. La energía se transmite a través del hielo por conducción. Como el agua cerca del hielo tiene una temperatura mayor que la del aire, la energía fluye del agua hacia el aire. Pero el agua cerca del hielo está a una temperatura de 0oC, por lo que al ceder energía sufre un cambio de fase y se congela. Este proceso hace aumentar el grosor de la capa de hielo.
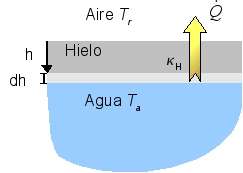
Veamos cuanto vale la potencia transferida a través del hielo. En este caso tenemos un medio homogéneo, similar a la barra homogénea del problema anterior. El papel de la longitud de la barra lo representa aquí el grosor de la capa de hielo h. Vamos a suponer que en cada instante la potencia de energía transferida es la misma en cada punto del hielo. En el problema anterior vimos que cuando el medio es homogéneo la temperatura varía linealmente. Entonces podemos hacer la aproximación
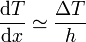
La potencia transferida a través del hielo es entonces
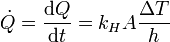
Aquí, kH es la conductividad térmica del hielo y A es la superficie del estanque. Podemos reescribir esta expresión de modo que obtenemos la energía cedida por el agua en el intervalo de tiempo dt
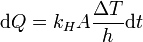
Ahora bien, está energía es la que ha cedido el agua al congelarse. Suponiendo que en el intervalo de tiempo dt se congela una fila lámina de agua de grosor dh, la energía cedida por el agua es
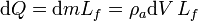
dV es el volumen de la lámina de agua que se ha congelado. Si la superficie del estanque es A este volumen es dV = Adh. Entonces la energía cedida por el agua en el tiempo dt es
dQ = ρaALfdh
Lf es el calor latente de fusión del agua.
Ahora podemos igualar el calor transferido a través del hielo con el calor cedido por el agua en el intervalo de tiempo dt
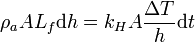
Esta es una ecuación diferencial en variables separables que podemos escribir
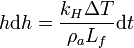
Integrando obtenemos
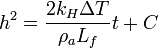
Para calcular la constante imponemos que para t = 0 el espesor de hielo es h0. Obtenemos finalmente
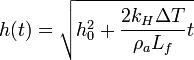
El tiempo necesario para que el grosor pase de h0 a hf es
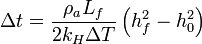
Para los datos del problema, tomando 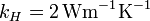 obtenemos
obtenemos